Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 71
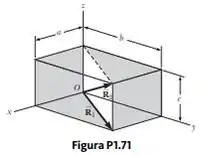
Um paralelepípedo retangular tem dimensões e , como mostrado na Figura P1.71.
a) Obtenha uma expressão para o vetor da face diagonal .
b) Qual é o módulo desse vetor?
c) Observe que , e formam um triângulo retângulo. Obtenha uma expressão para o vetor diagonal do corpo .
Passo 1
a) A expressão que identifica um vetor, no caso , são as coordenadas desse vetor no espaço. Como na figura a gente tem os eixos , , e , nessa ordem, a expressão pra vai ser:
Passo 2
b) A formulinha pro módulo de um vetor qualquer, que vale a pena que você saiba de cor, é a seguinte:
Em que , e representam as coordenadas desse vetor, nos eixos , e respectivamente.
Assim, pro vetor , a gente vai ter o seguinte
Passo 3
c) Da mesma forma que em a), observando a figura a gente consegue determinar as coordenadas do vetor . Vamos ter o seguinte:
Resposta
a)
b)
c)