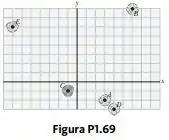
Um pirata enterrou seu tesouro em uma ilha com cinco árvores localizadas nos pontos , , , e , todos medidos em relação a uma origem na Figura P1.69. O registro do seu navio instrui a começar pela árvore A e se mover em direção à árvore B, mas percorrer apenas metade da distância entre A e B. Então, mova-se em direção à árvore C, cobrindo um terço da distância entre sua localização atual e C. Em seguida, mova-se para a árvore para D, cobrindo um quarto da distância entre onde ele está e D. Por fim, mova-se para a árvore E, cobrindo um quinto da distância entre ele e E, pare e cave.

a) Considere que você determinou corretamente a ordem na qual o pirata identificou as árvores como A, B, C, D e E como mostrado na Figura. Quais são as coordenadas do ponto onde ele enterrou o tesouro?

b) E se? E se você realmente não souber a maneira como o pirata identificou as árvores? O que aconteceria com a resposta se você rearranjasse a ordem das árvores, por exemplo, para B , A , E , C e D ? Indique o raciocínio para mostrar que a resposta não depende da ordem na qual as árvores foram identificadas.

Agora, o deslocamento de sua posição atual para C é:

Você cobre um terço, movendo-se para:

O deslocamento de onde você está para D é:

Você atravessa um quarto dele, movendo-se para:

O deslocamento de sua nova localização para E é:

dos quais você cobre um quinto da distância,, se movendo para:

O tesouro está em.

Letra b:

Seguir as instruções leva você à posição média das árvores. As etapas que seguimos numericamente na parte (a) levam você a:

E depois,

E depois,

E por fim,

Esse centro de massa da distribuição da árvore é o mesmo local seja qual for a ordem em que pegamos as árvores.