Teoria
A lei de Lenz diz que “o sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito”.
O que é a Lei de Lenz?
A Lei de Lenz existe pra responder uma pergunta que Faraday não conseguiu responder lá na Lei de Faraday!
O negócio é o seguinte:
Segundo Faraday a variação do fluxo magnético
Na prática, a variação do fluxo magnético
O que Faraday não conseguiu responder foi, como o sentido da corrente induzida varia. E ai entra a Lei de Lenz!
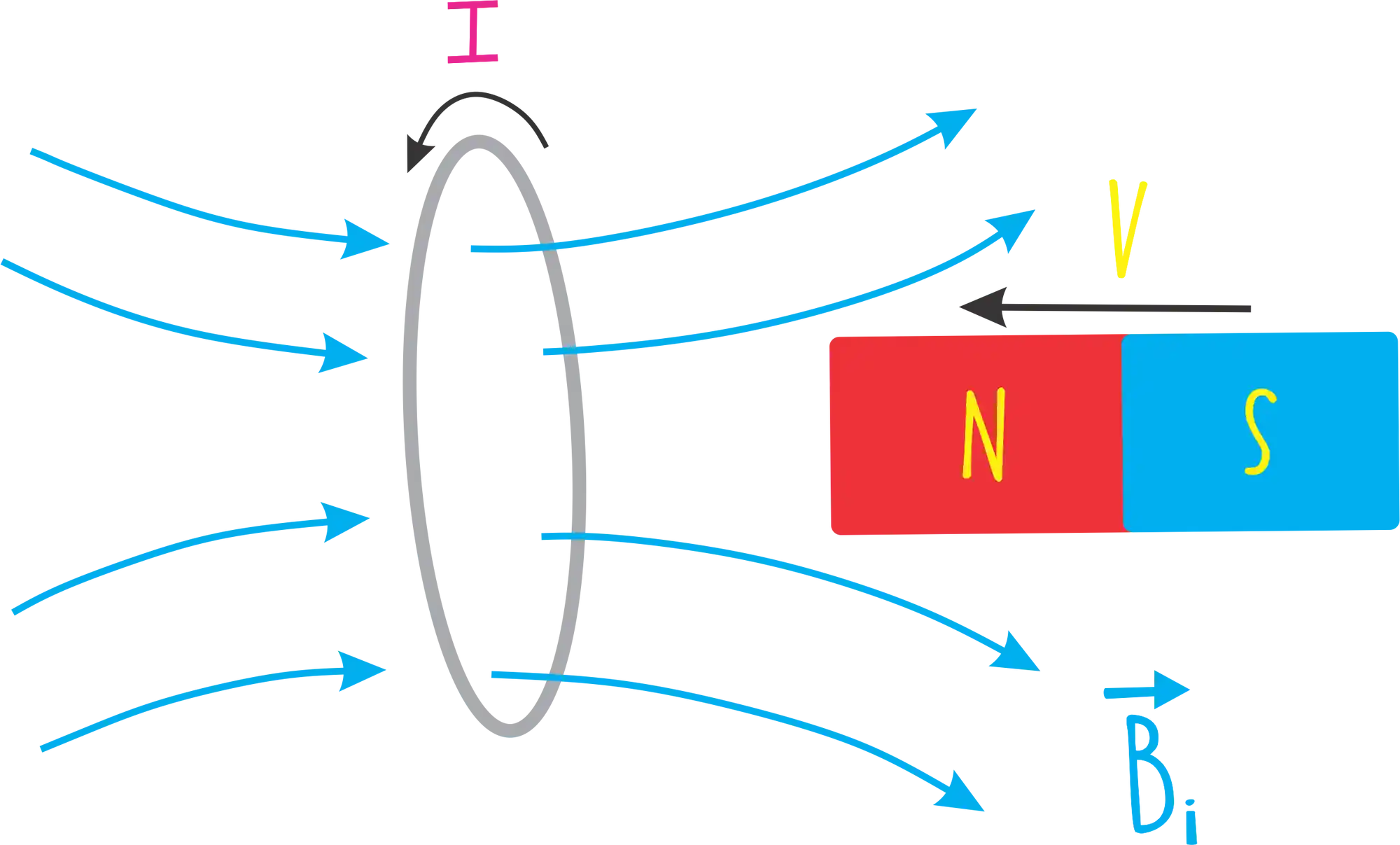
Recapitulando… Se a gente aproxima um imã de uma espiral estamos variando o Fluxo do Campo Magnético
Ou seja, vai ser criado um campo magnético induzido
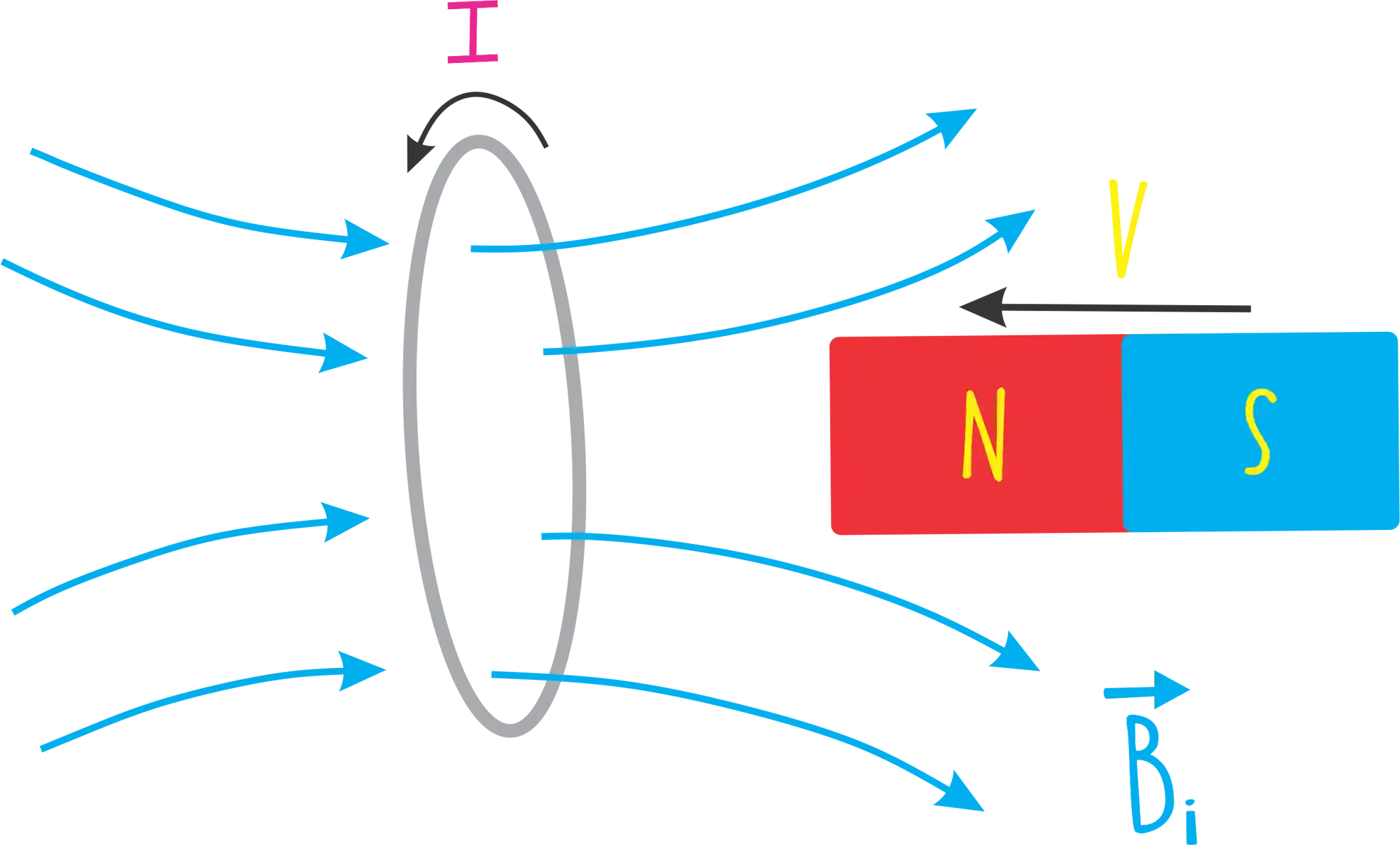
Pra descobrirmos a direção dessa corrente induzida, usamos a Regra da Mão Direita!
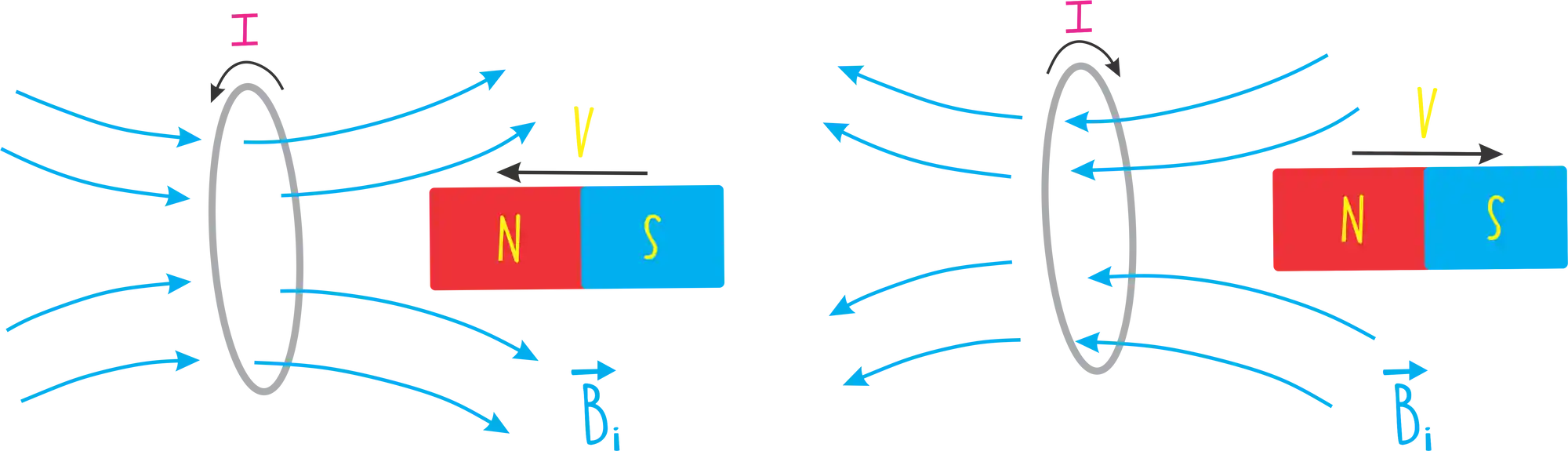
Agora, e se a gente afastar o imã?
Nesse caso também estamos variando o campo magnético, mas o campo magnético induzido
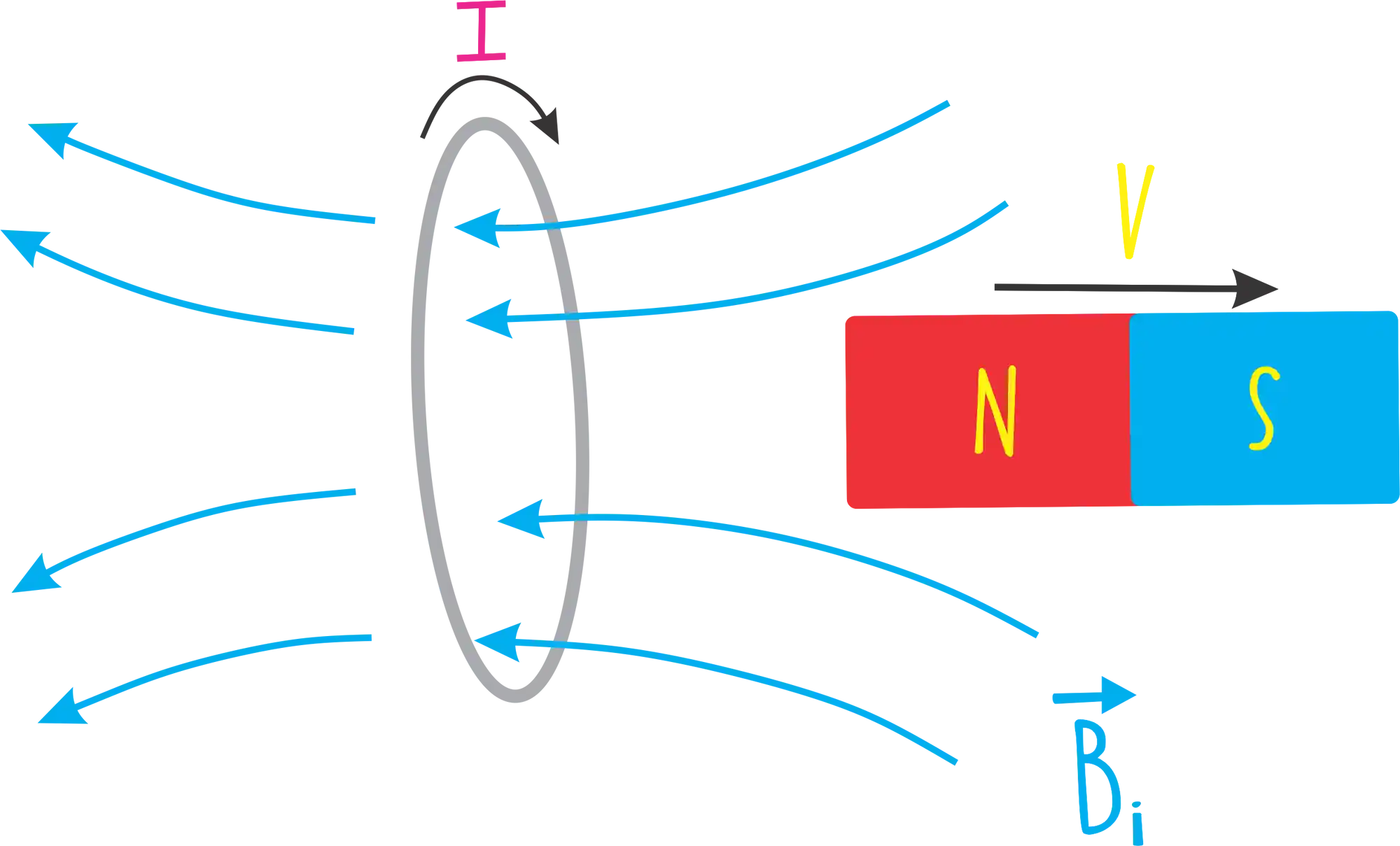
De novo, fazemos a regra da mão direita e descobrimos o sentido da corrente induzida!
Lei de Faraday
A gente já falou um pouco sobre a Lei de Faraday, mas agora vamos entender melhor como ela funciona!
Como vimos, lá em cima, a Lei de Faraday diz que a variação do Fluxo do Campo Magnético
Matematicamente podemos escrever:
Onde:
é Força eletromotriz induzida (volts) ; é o Fluxo do campo magnético pela área do circuito.
Campo Elétrico Induzido
Se a variação de fluxo magnético através de uma espira vai fazer com que surja uma corrente elétrica induzida, necessariamente fará com que surja um campo elétrico induzido também!
Por definição, a
Substituindo na Lei de Faraday, teremos:
Onde a integral de linha é executada através de uma curva fechada.
A curva da integral pode ser uma curva imaginária, isso permite calcular o campo elétrico induzido gerado em qualquer ponto do espaço. Vamos trabalhar isso nos exercícios
Lei de Lenz: Vídeo Aula
Agora se liga nessa vídeo aula completíssima sobre Lei de Lenz 👇
É isso, galera! Vamos pôr as mãos na massa agora!
Lei de Faraday
Lei de Lenz: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 293-1.
Na figura abaixo o fluxo de campo magnético na espira aumenta de acordo com a equação , onde está em miliwebers e em segundos.
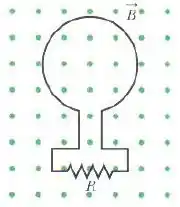
Qual é o módulo da força eletromotriz induzida na espira no instante ?
O sentido da corrente no resistor é para a direita ou para a esquerda?
Passo 1
Qual é o módulo da força eletromotriz induzida na espira no instante ?
Por definição:
Jogando a função na equação acima, teremos:
Para :
Portanto
Obs.: Se você estiver se perguntando porque a induzida ficou em milivolts , lembre que o enunciado nos disse que o fluxo magnético está em miliwebers . ;)
Passo 2
O sentido da corrente no resistor é para a direita ou para a esquerda?
De acordo com a lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela quer dizer é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Show!
A variação do fluxo magnético será:
Em :
Assim, como o fluxo está aumentando, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo, ou seja, entrando na sua tela.
Usando a regra da mão direita, vemos que a corrente induzida vai estar no sentido horário.
Resposta
A corrente induzida vai estar no sentido horário.
Exercício Resolvido #2
UFRJ – Prova 2 – 2014.1 – Questão Discursiva nº2.
Um pedaço de fio condutor ôhmico isolado é torcido de modo a constituir um circuito em forma de oito. Por razão de simplicidade, modele as duas metades da figura de oito como circunferências de círculo. O raio do círculo superior é e o do inferior é . O circuito completo é puramente resistivo (com capacitância e autoindutância desprezíveis), tendo resistência . A partir de um campo magnético uniforme, mas não estacionário
Onde é aplicado perpendicularmente ao plano dos dois circuitos, conforme mostrado na figura.
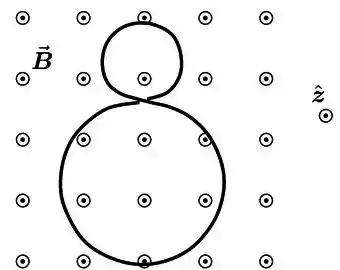
- Para determino o fluxo total através do circuito.
- Para determine o sentido da corrente elétrica induzida ao longo do fio indicando-o claramente em cada uma das circunferências, seja por intermédio de uma seta, seja pelas expressões horário ou anti-horário.
- Para determine o módulo da intensidade da corrente elétrica induzida no fio.
Passo 1
O fluxo é dado pela integral:
Onde é a superfície toda do circuito. Note que quando ele pega um arame normal e “torce” ele passa a ter duas orientações da normal:
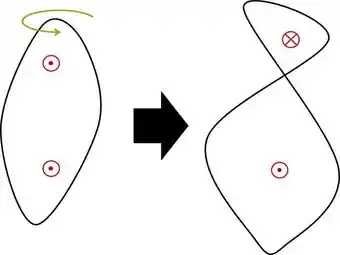
Fazendo o fluxo, podemos separar em duas integrais, onde cada uma tem um vetor normal constante. Seja a de raio maior a com e a outra no sentido de .
Pondo as constantes (digo constantes em relação às variáveis de integração, que são de espaço) para fora:
Segue:
Podemos ver que o fluxo total aumenta com o tempo.
Passo 2
Pela Lei de Lenz, como temos um fluxo aumentando no sentido de , o efeito induzido vai tentar compensar este fato. Por conta disto, pela regra da mão direita podemos ver que será induzida uma corrente que, no círculo maior, é horária:
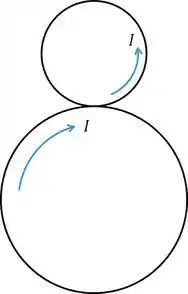
Naturalmente, no menor vai ser anti-horária.
Passo 3
Para calcular a intensidade da corrente induzida vamos rodar a Lei de Faraday:
E juntar com a Lei de Ohm:
De forma que:
Derivando o fluxo:
O módulo da corrente fica então:
Resposta
a)
b)
Anti-horária no menor e horária no maior.
c)
Exercício Resolvido #3
UFRJ – Prova 2 – 2014.2 – Múltipla Escolha nº7.
Uma espira circular move-se de baixo para cima na direção de um imã permanente fixo, assim como na figura abaixo.
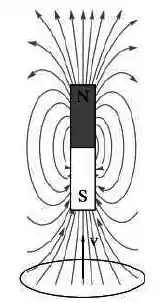
Vista de cima a corrente no fio será:
no sentido horário e a força na espira será para cima
no sentido anti-horário e a força na espira será para cima
no sentido horário e a força na espira será para baixo
no sentido anti-horário e a força na espira será para baixo
no sentido horário e a força na espira será zero
no sentido anti-horário e a força na espira será zero
Passo 1
De acordo com a lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela quer dizer é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Assim, conforme aproximamos a espira do imã, vamos aumentando o fluxo magnético através da espira, assim, o campo magnético induzido vai estar no sentido contrário ao campo magnético do imã. Ou seja, apontando para baixo.
Para que o campo magnético induzido na espira aponte para baixo é necessário que, vista de cima, a corrente induzida esteja no sentido horário.
Passo 2
Como o campo magnético induzido na espira está no sentido contrário ao campo magnético do imã, haverá uma força de repulsão entre os dois. Assim, a força sobre a espira será para baixo.
A resposta certa é a letra .
Resposta
no sentido horário e a força na espira será para baixo
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 297-36.
A figura abaixo mostra duas regiões circulares, e , de raios e .
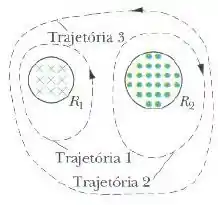
Em existe um campo magnético uniforme de módulo dirigido para dentro do papel, e em existe um campo magnético uniforme de módulo dirigido para fora do papel (ignore os efeitos de borda).
Os dois campos estão diminuindo à taxa de . Calcule o valor de para a trajetória 1; para a trajetória 2; para trajetória 3.
Passo 1
Calcule o valor de para a trajetória 1;
De acordo com a Lei de Faraday:
Usando a regra da mão direita, vemos que a orientação da trajetória 1 está no sentido contrário ao campo magnético em , logo:
Onde:
Logo:
Passo 2
Calcule o valor de para a trajetória 2;
De acordo com a Lei de Faraday:
Usando a regra da mão direita, vemos que a orientação da trajetória 2 está no sentido contrário ao campo magnético em , logo:
Onde:
Logo:
Passo 3
Calcule o valor de para a trajetória 3;
Vemos que a trajetória 3 tem a mesma orientação da trajetória 1 e orientação contrária à trajetória 2. Portanto:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-37.
Um solenóide longo tem um diâmetro de . Quando o solenóide é percorrido por uma corrente , um campo magnético uniforme de módulo é produzido no seu interior.
Através de uma diminuição da corrente o campo magnético é reduzido a uma taxa de . Determine o módulo do campo elétrico induzido a e a a de distância do eixo do solenóide.
Passo 1
Determine o módulo do campo elétrico induzido a de distância do eixo do solenóide.
Pela Lei de Faraday, temos que:
Como a área é constante e o campo magnético é uniforme, podemos reescrever a equação acima da seguinte forma:
Como estamos calculando o campo elétrico induzido no interior do solenóide, a área transversal será um círculo, e a curva fechada que usaremos na integral é a curva circular que contorna . Logo, podemos reescrever a equação acima da seguinte forma:
Onde:
Logo:
Passo 2
Determine o módulo do campo elétrico induzido a de distância do eixo do solenóide.
Aqui vamos usar o mesmo princípio, mas como estamos calculando o campo elétrico induzido em um ponto fora do solenóide, a área será , onde é o raio do solenóide.
Logo:
Onde:
Logo:
Resposta
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-38.
Uma região circular no plano é atravessada por um campo magnético uniforme orientado no sentido positivo do eixo . O módulo do campo (em teslas) aumenta com o tempo (em segundos) de acordo com a equação , onde é uma constante.
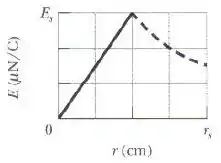
A figura acima mostra o módulo do campo elétrico criado por esse aumento do campo magnético em função radial ; a escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .
Determine o valor de .
Passo 1
Pela Lei de Faraday, temos que:
Como a área é constante e o campo magnético é uniforme, podemos reescrever a equação acima da seguinte forma:
Como estamos calculando o campo elétrico induzido no interior do solenóide, a área transversal será um círculo, e a curva fechada que usaremos na integral é a curva circular que contorna . Logo, podemos reescrever a equação acima da seguinte forma:
Onde, entre :
Logo:
Passo 2
Para , , logo:
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 298-39.
O campo magnético de um imã cilíndrico com de diâmetro varia senoidalmente entre e com uma frequência de .
Qual é a amplitude do campo elétrico induzido por essa variação a uma distância de do eixo cilíndrico?
Passo 1
Como o campo magnético varia senoidalmente, ele vai ter mais ou menos essa cara:
Onde:
Passo 2
Pela Lei de Faraday, temos que:
Como a área é constante e o campo magnético é uniforme, podemos reescrever a equação acima da seguinte forma:
Como estamos calculando o campo elétrico induzido no interior do solenóide, a área transversal será um círculo, e a curva fechada que usaremos na integral é a curva circular que contorna . Logo, podemos reescrever a equação acima da seguinte forma:
Passo 3
Jogando o campo magnético na expressão do campo elétrico, teremos:
A amplitude do campo elétrico induzido, ou o campo elétrico máximo é dado por:
Onde .
Onde:
Logo:
Resposta
Exercício Resolvido #8
Site do Prof. A. F. Guimarães, lista 09 de Física 3
Uma espira circular de de diâmetro, feita de fio de cobre nº 10 (diâmetro igual a ), é colocada num campo magnético uniforme de modo que o seu plano fique perpendicular ao vetor . Qual deve ser a taxa de variação de com o tempo para que a corrente induzida na espira seja igual a ? Assuma que a resistividade do cobre vale
Passo 1
A resistência da espira será dada por:
em que e e é o raio da espira e é o raio do fio de cobre.
Para a força eletromotriz, temos:
Substituindo uma equação na outra, teremos:
Passo 2
Como
onde é a área atravessada pelo campo, dada por
Temos que:
Vamos assumir aqui apenas o módulo de , logo:
Passo 3
Substituindo os valores numéricos, temos que:
Resposta
Exercício Resolvido #9
Site do Prof. A. F. Guimarães, lista 10 de Física 3
Faz-se girar uma bobina retangular, contando espiras de comprimento e largura , com uma frequência na presença de um campo magnético uniforme , como mostra a figura abaixo.
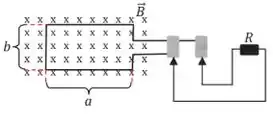
(a) Mostre que a f.e.m. induzida que aparece na bobina é dada por:
(b) Projete uma bobina para a qual seja igual a , quando girada revoluções por segundo, na presença de um campo magnético de
Passo 1
(a) Mostre que a f.e.m. induzida que aparece na bobina é dada por:
O fluxo do campo magnético é dado por:
em que
Já a f.e.m. é dada por:
onde é o número de espiras.
Assim sendo, utilizando as equações acima, chegamos em:
Passo 2
(b) Projete uma bobina para a qual seja igual a , quando girada revoluções por segundo, na presença de um campo magnético de
Para os valores do enunciado, temos que:
Resposta
(b)
Exercício Resolvido #10
Site do Prof. A. F. Guimarães, lista 10 de Física 3
A figura abaixo mostra duas espiras de fio em forma de anel, que tem o mesmo eixo. O anel menor está acima do maior, a uma distância que é grande, comparada com o raio , do anel maior. Em consequência, com a passagem da corrente pelo anel maior (veja figura), o campo magnético correspondente é aproximadamente constante através da área plana , limitada pelo anel menor. Suponha agora que a distância não seja fixa, mas que varie na razão constante
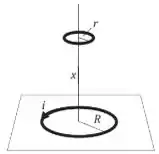
(a) Determinar o fluxo magnético através da área limitada pelo anel menor em função de .
(b) Calcular a f.e.m. gerada no anel menor, no instante em que for igual a .
(c) Determinar o sentido da corrente induzida no anel menor, se .
Passo 1
(a) Determinar o fluxo magnético através da área limitada pelo anel menor em função de .
O módulo do vetor indução magnética promovito por uma corrente em uma espira circular a uma distância do seu centro é dado por:
No entanto, para , teremos que:
Assim, para o fluxo, teremos que:
Passo 2
(b) Calcular a f.e.m. gerada no anel menor, no instante em que for igual a .
A taxa de variação do fluxo é dada por:
Logo, a força eletromotriz será dada por:
Por fim, para , temos que:
Passo 3
(c) Determinar o sentido da corrente induzida no anel menor, se .
Para , temos . Assim, a corrente induzida na espira menor terá o mesmo sentido da corrente da espira maior.
Resposta
(a)
(b)
(c) Mesmo sentido da corrente da espira maior.