Ondas de Choque e Cone de Mach
Teoria
Fala aí! Hoje vamos aprender sobre o Cone de Mach, que é um efeito observado quando uma fonte sonora se desloca no espaço com velocidade maior do que a do som.
Bora ver como funciona isso aí?
Veja também:
O que é o Cone de Mach?
Se um corpo gerador de ondas mecânicas viaja a uma velocidade maior do que a das próprias ondas que ele produz, as ondas produzidas vão se restringir aos limites da figura de um cone. Este é conhecido como cone de Mach.
Vamos imaginar algumas situações pra ilustrar essa ideia melhor. Pra começar, imagine uma fonte emissora de ondas parada, pode ser um carro qualquer, por exemplo.
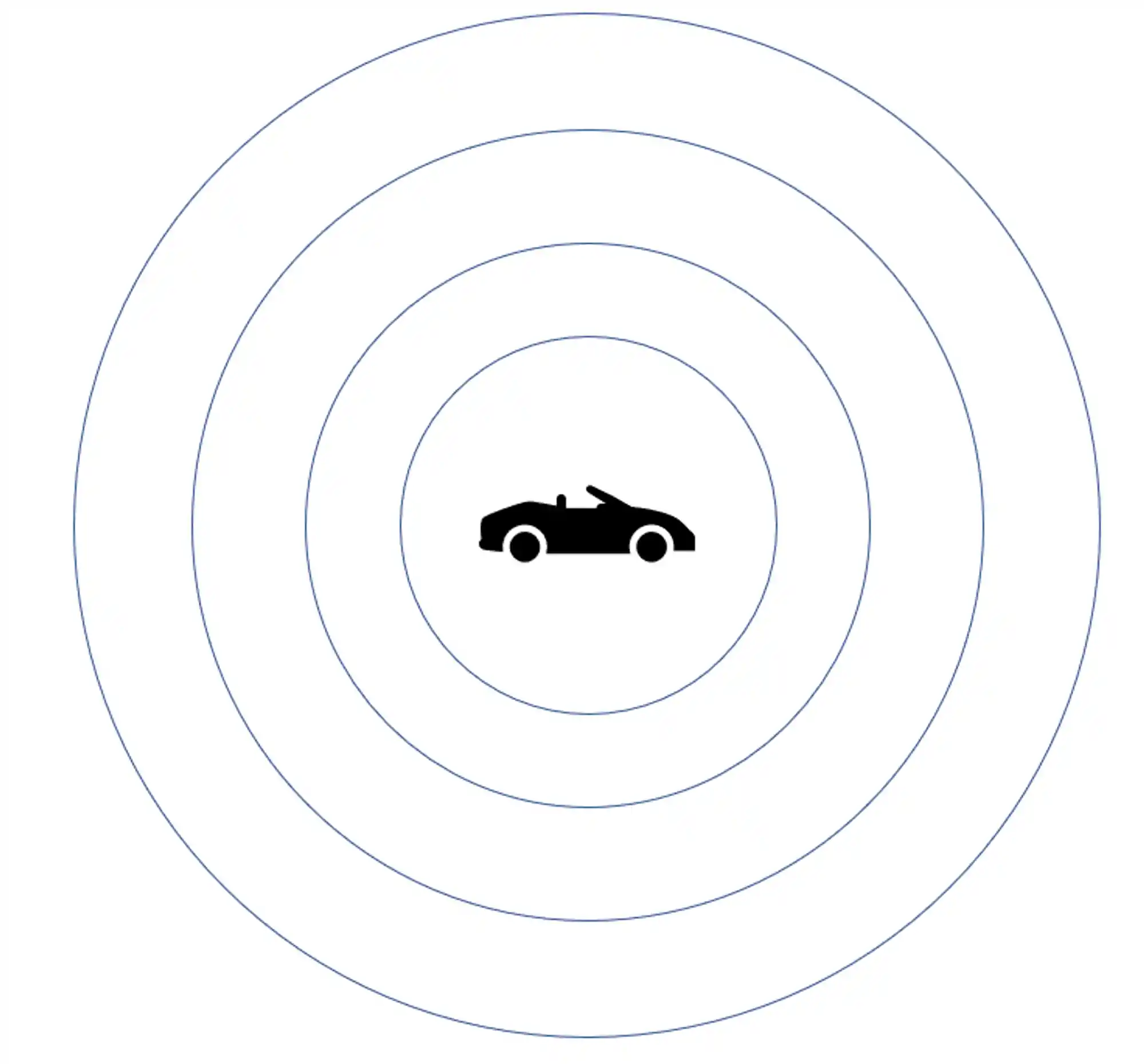
Se quiser entender melhor por que eu desenhei as ondas como esses círculos assim, dá uma conferida nesse conteúdo aqui. Lá eu te conto tudinho sobre como as ondas sonoras se propagam 😉
As frentes da onda vão crescer em todas as direções do espaço e, como a origem (o carro) está parada, vão se distanciar uniformemente da fonte, beleza?
Agora, imagine que esse carro comece a se mover para a direita bem devagarzinho.
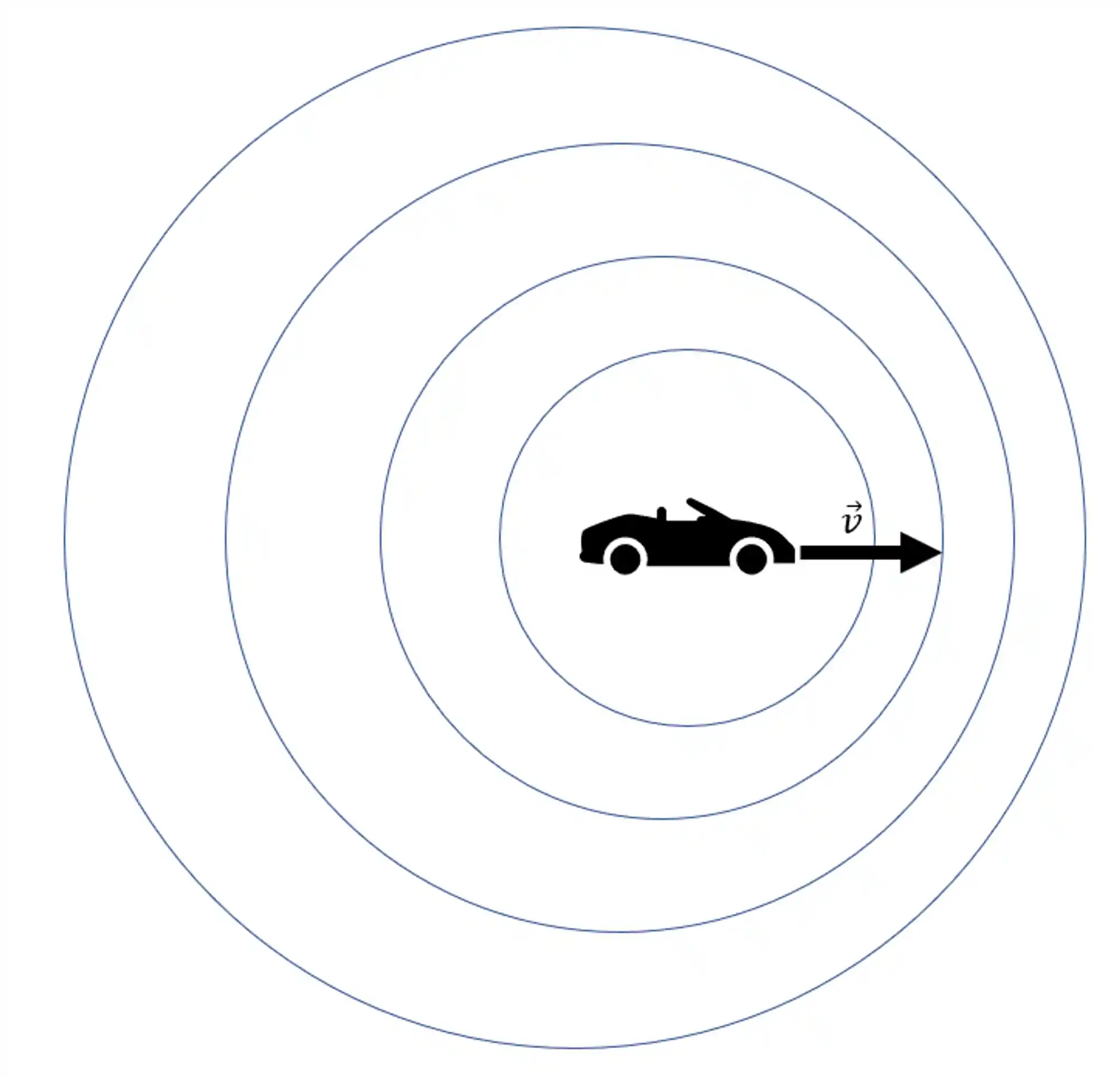
As frentes de onda (as linhas circulares) continuam se distanciando da fonte, mas agora de maneira não uniforme. Olha só, como o carro tá se movendo para a direita, as frentes de onda ali do lado direito (na frente do carro) vão estar muito mais próximas umas das outras do que aquelas atrás do carro.
É como se cada onda ali do lado direito estivesse se deslocando a uma velocidade
Tá, seguindo em frente. Agora, vamos trocar nosso humilde carrinho por um mais rápido, que se desloca com a velocidade do som!
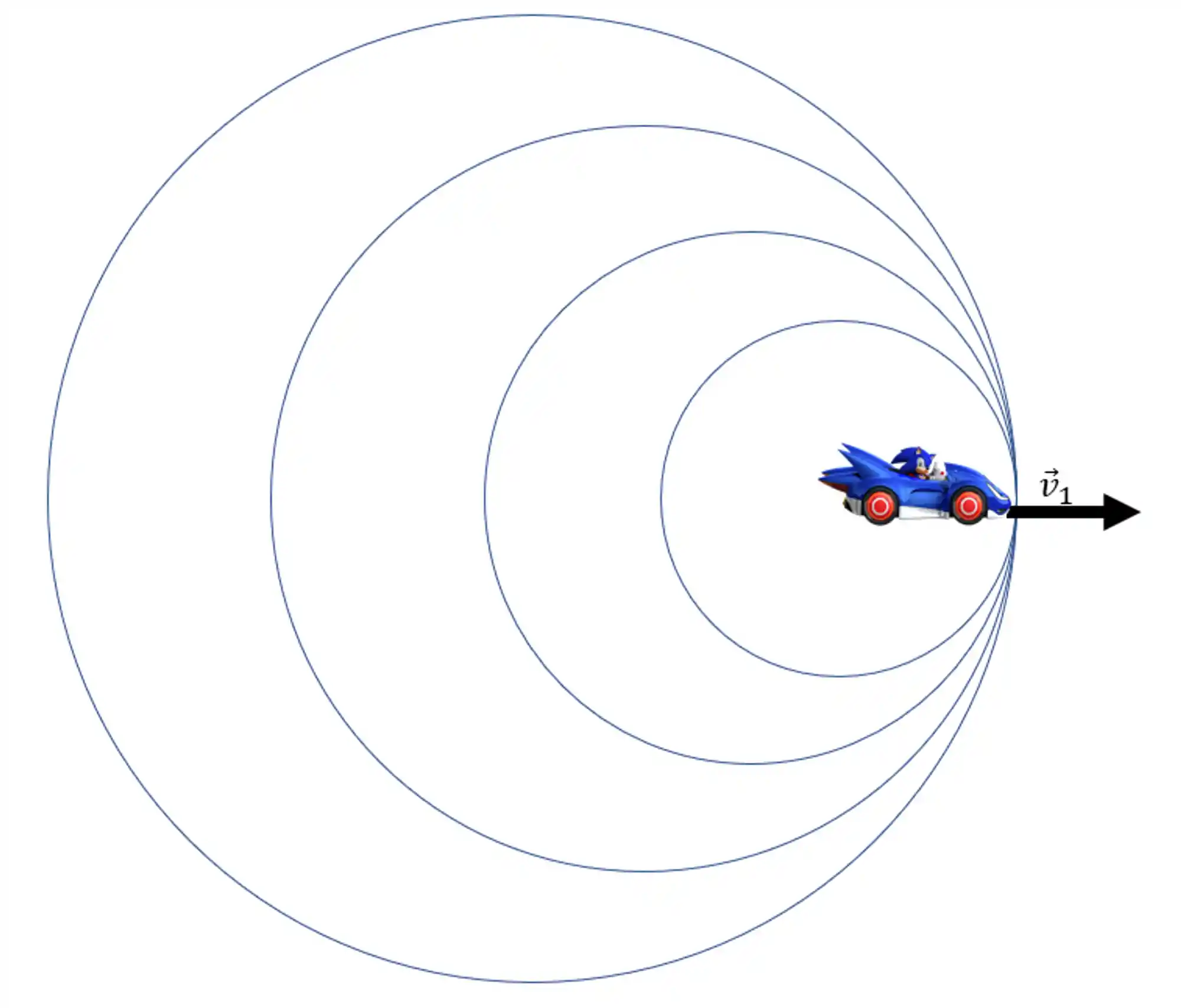
O que tá acontecendo aqui? Ora, se nosso carro tá se movendo à velocidade do som, as frentes de onda ali do lado direito não conseguem se afastar dele, porque elas têm a mesma velocidade que o próprio carro!
Agora chegamos na nossa última situação, que é a que mais nos interessa aqui:
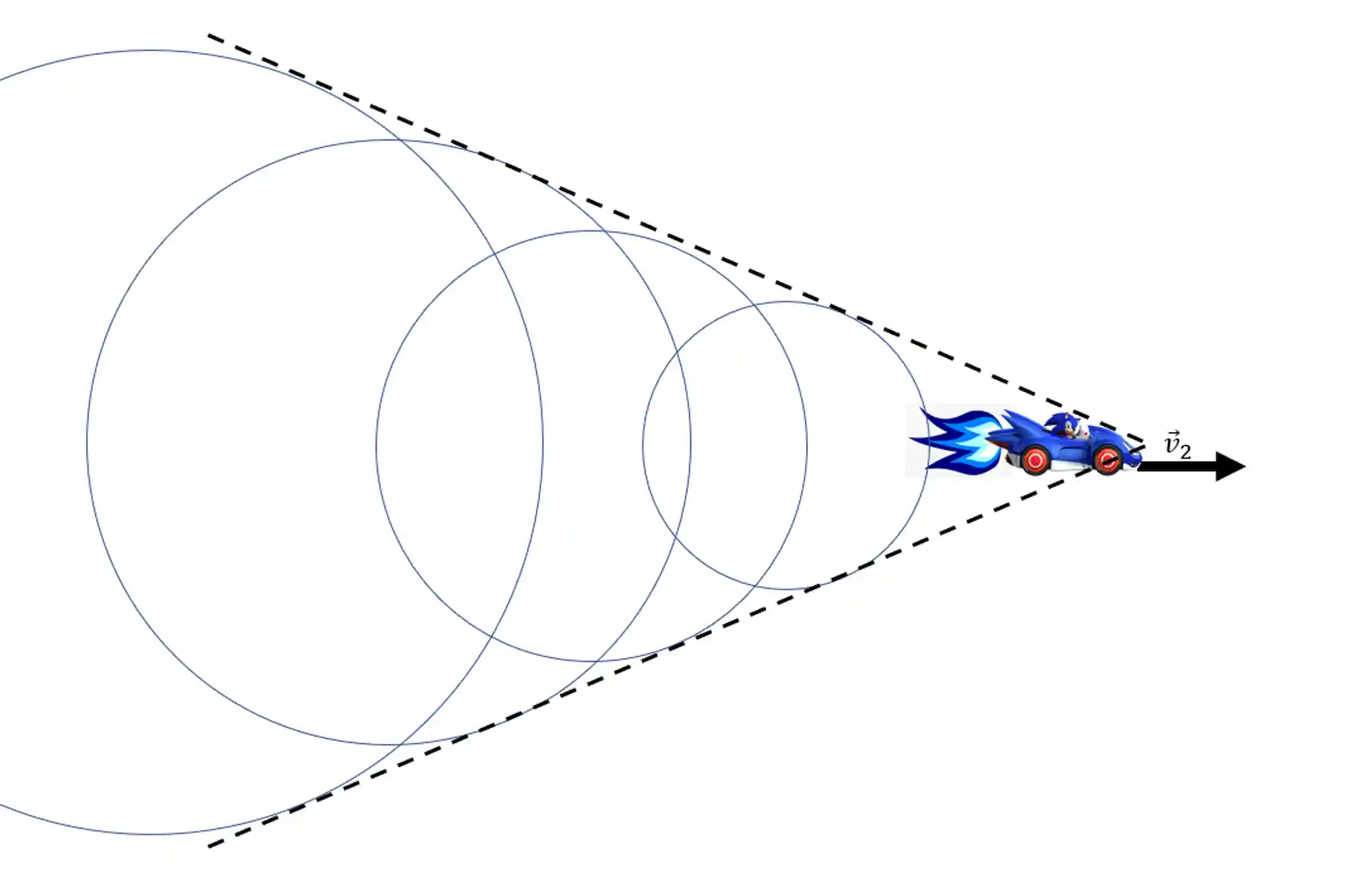
Dessa vez, o carrinho tá se movendo a uma velocidade supersônica (velocidade maior que a do som). Por isso as ondas sonoras não conseguem acompanhá-lo e vão ficando pra trás.
Percebeu a figura que aquelas linhas tracejadas ali formam? Aquele é o tal do Cone de Mach!
Se você tiver mais facilidade em aprender com vídeos, dá só uma olhada nesse aqui bem explicadinho pra você:
Número de Mach
O número de Mach é uma relação que indica quantas vezes a velocidade de uma fonte é maior que a velocidade do som (a velocidade Mach).
Agora que já entendemos o conceito desse tal cone de Mach, vamos adotar um olhar mais matemático.
Tirei o carrinho do Sonic dessa última figura e adicionei alguns detalhes, olha só:
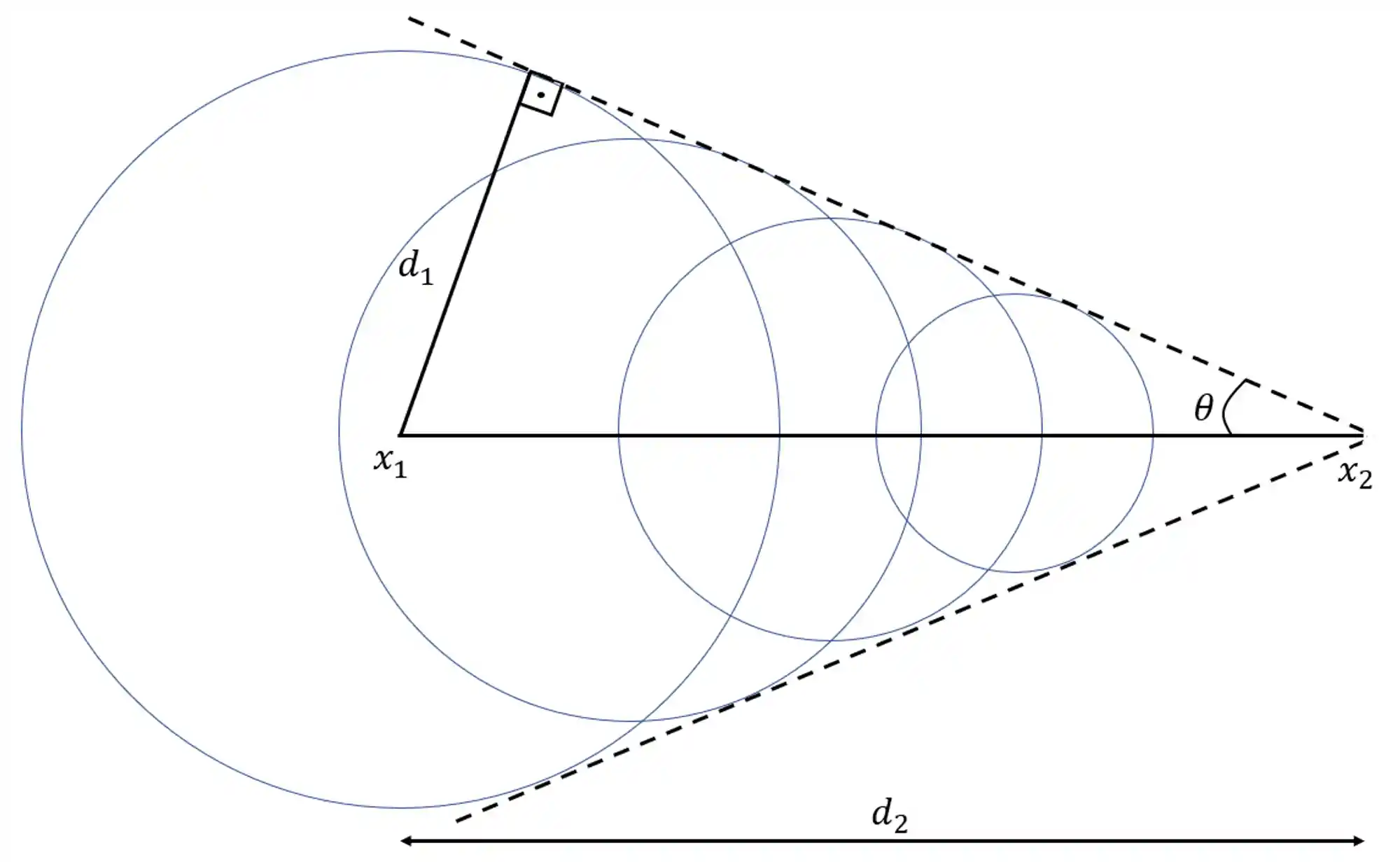
Legenda:
é a posição no espaço em que a fonte se encontrava quando gerou a primeira onda. é a posição atual da fonte geradora. é a distância entre o centro da primeira onda e o ponto em que o cone de Mach tangencia a onda. é a distância que a fonte percorreu desde que gerou a primeira onda. é o semiângulo da abertura do cone.
Como a gente pode encontrar o valor daquele ângulo
Podemos tirar uma relação daquele triângulo retângulo mostrado ali! Olha só, o seno do ângulo é igual ao cateto oposto sobre a hipotenusa:
E como a gente encontra
Essa é a distância que a frente da onda percorreu desde que foi gerada, certo? Vamos dizer que se passou um tempo
E
É a distância que a fonte, o carrinho, percorreu nesse mesmo intervalo de tempo.
Com isso, podemos reescrever nosso seno do ângulo.
Se tomarmos o inverso dessa relação, chegamos à relação que queremos:
Essa razão
Quando você ouvir uma notícia de que um avião Mach 5 está sendo desenvolvido, isso quer dizer que esse avião é capaz de voar com uma velocidade 5 vezes maior que a do som!
Perceba ainda que este número é diretamente proporcional à velocidade da fonte, mas inversamente proporcional ao ângulo! Então, quanto maior a velocidade da fonte, mais fechadinho vai ser o cone de Mach formado.
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 88
Uma bala é disparada com uma velocidade de . Determine o ângulo entre o cone de choque e a trajetória da bala.
Passo 1
Simples, vamos usar a fórmula:
Usando a velocidade do som como , o enunciado diz que :
Resposta
Exercício Resolvido #2
Num universo paralelo qualquer, o Flash resolveu brincar de pique-pega com o Flecha.
Num primeiro momento, o Flecha estava correndo a uma velocidade de , enquanto o Flash estava a uma velocidade de . Determine a razão dos ângulos entre o cone de choque do Flash com o ângulo do cone de choque do Flecha.
Passo 1
Simples, vamos usar a fórmula:
Usando a velocidade do som como , temos para o Flash:
Já para o Flecha:
Looogo,
Resposta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume 2: ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 68
A onda de choque produzida por um avião tinha um ângulo de aproximadamente . O avião estava se movendo a no momento em que a fotografia foi tirada. Qual era, aproximadamente a velocidade do som na altitude do avião?
Passo 1
Usando a fórmula do cone de Mach:
Queremos descobrir o valor da velocidade do som , portanto:
Resposta
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 69
Um avião a jato passa sobre um pedestre a uma altitude de e uma velocidade de Mach 1,5. (a) determine o ângulo do cone de Mach (a velocidade do som é ). (b) Quanto tempo após o avião ter passado diretamente acima do pedestre ele é atingido pela onda de choque?
Passo 1
- Aqui, nos basta aplicar a fórmula do cone de Mach:
- Vamos fazer um desenho:
Passo 2
A distância é a distância percorrida pelo avião após passar por cima do pedestre, pela imagem temos:
Resposta
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 70
Um avião voa a vez a velocidade do som. Seu estrondo sônico atinge um homem no solo min depois de o avião ter passado exatamente por cima dele. Qual é a altitude do avião? Suponha que a velocidade do som é .
Passo 1
Vamos fazer um desenho:
Se usarmos a fórmula do cone de Mach, conseguiremos o valor de , se liga:
Nós já temos o valor de , foi dado no enunciado que é de . Portanto:
Fazendo as continhas: