Refração em Interfaces Esféricas
Teoria
Esse capítulo é voltado para situações em que uma superfície esférica (com centro de curvatura e raio de curvatura ) separa dois meios diferentes.
Dessa forma, a luz emitida por um objeto pontual em um meio com índice de refração incidirá sobre a interface esférica com um meio de índice de refração . Como mostra a figura:
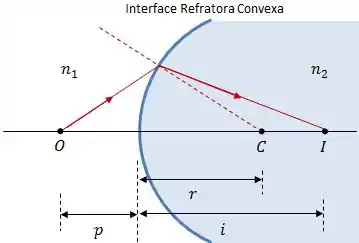
Atenção! As imagens formadas por refração em uma interface são virtuais quando estão do mesmo lado que o objeto e reais quando estão do lado oposto. Ou seja, é o contrário do que estávamos acostumados quando estudamos espelhos esféricos.
Então, cuidado para não dar mole com isso.
A relação entre os parâmetros mostrados na imagem acima é dada por:
Lembrando que, assim como em espelhos planos, definimos que o valor de será negativo para imagens virtuais, e será positivo para imagens reais. Além disso, o valor de será sempre positivo.
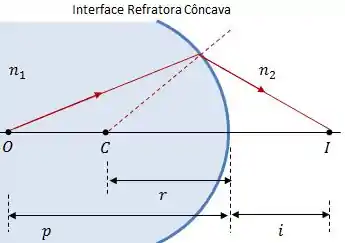
Quando o objeto estiver diante de uma interface refratora convexa o raio de curvatura será positivo, e quando ele estiver diante de uma interface côncava o raio de curvatura será negativo.
A imagem abaixo mostra uma interface refratora côncava.
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 66
Uma esfera de vidro de raio tem um índice de refração de . Um peso de papel com uma altura é fabricado cortanto a esfera ao longo do plano situado a do centro da esfera.
O peso de papel é colocado sobre uma mesa e visto por um observador situado a uma distância da superfície da mesa.
A que distância a superfície da mesa parece estar do observador?
Passo 1
Como queremos saber a que distância a superfície da mesa parece estar do observador, vamos começar considerando que é como se o nosso real observador estivesse sobre a mesa.
Vamos usar a seguinte equação:
Nesse caso, como o real observador está na mesa, teremos que:
Substituindo na equação, teremos:
Passo 2
Baseado no valor que encontramos acima, o que vai acontecer é que, o observador vai parecer estar a uma distância dada por:
Resposta
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 66
A figura abaixo um feixe de raios luminosos paralelos produzidos por um laser incide em uma esfera maciça transparente de índice de refração .
Se uma imagem pontual é produzida na superfície posterior da esfera, qual é o índice de refração da esfera?
Existe algum valor do índice de refração para o qual é produzida uma imagem pontual do centro da esfera? Se a resposta for afirmativa, qual é esse valor?
Passo 1
Se uma imagem pontual é produzida na superfície posterior da esfera, qual é o índice de refração da esfera?
Se a imagem é formada na superfície posterior da esfera, temos que . Além disso, como não sabemos exatamente onde está o laser e os raios chegam paralelos, podemos considerar . Logo:
Onde o meio 1 é o ar, com índice de refração . Logo:
Passo 2
Existe algum valor do índice de refração para o qual é produzida uma imagem pontual do centro da esfera? Se a resposta for afirmativa, qual é esse valor?
Para que a imagem esteja no centro da esfera, basta fazer :
Isso só seria possível se ou . Logo, não existe valor do índice de refração para o qual é produzida uma imagem pontual no centro da esfera.
Resposta
Não existe valor do índice de refração para o qual é produzida uma imagem pontual no centro da esfera.
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 66-67
Um objeto está sobre o eixo central de uma superfície refratora esférica. Para cada problema a tabela abaixo mostra o índice de refração do meio em que se encontra o objeto, o índice de refração do outro lado da superfície refratora, a distância do objeto , o raio de curvatura da superfície e a distância da imagem .
Determine os dados que faltam incluindo se a imagem é real ou virtual e se a imagem fica do mesmo lado da superfície que o objeto ou do lado oposto .
Atenção! Considere os dados referentes ao problema 34.
Passo 1
Os dados fornecidos pela tabela são:
Passo 2
A distância do objeto .
Para determinar o valor de , podemos usar a seguinte equação:
Reorganizando os termos, temos que:
Substituindo os valores, teremos:
Passo 3
Determine os dados que faltam incluindo se a imagem é real ou virtual .
A gente precisa olhar o valor da distância da imagem em relação ao espelho , como ela é positiva, significa que a imagem é real .
Passo 4
Determine os dados que faltam incluindo se a imagem fica do mesmo lado da superfície que o objeto ou do lado oposto .
Como a imagem é real, significa que ela se forma do lado oposto à superfície refratora esférica .
.
Resposta
A imagem é virtual .
A imagem se forma do mesmo lado que o objeto .