Refração
Teoria
Quando estudamos Ondas Eletromagnéticas, usamos a luz como exemplo para várias situações.
Entretanto, a natureza ondulatória da luz não é o suficiente para explicar tudo relacionado a ela.
Muitos eventos associados à emissão e absorção da luz revelam um comportamento corpuscular da luz, em que ela age como uma partícula.
Entendendo a Refração
A Refração ocorre quando um raio incide sobre uma superfície, que separa dois meios, formando um ângulo com a normal e, ao invés de ser refletido, o raio passa de um meio para o outro, agora formando um raio com a normal.
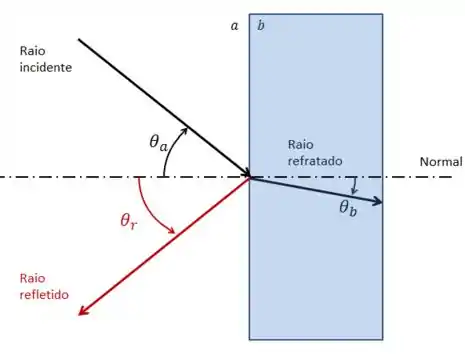
Quando uma onda de luz atinge uma superfície lisa separando dois meios transparentes e , geralmente uma parte da luz é refletida e uma parte da luz é refratada.
É por isso que, por exemplo, quando você está na rua e olha através do vidro para dentro de uma loja, você observa a reflexão da rua (reflexão) e o que está no interior da loja (refração).
O índice de refração
O índice de refração de um material () possui grande importância no estudo da ótica geométrica. Ele é dado por
Onde é a velocidade da luz no vácuo, que vale aproximadamente , e é a velocidade da luz no interior do material.
Assim, quanto maior o índice de refração, menor será a velocidade da luz no material.
No vácuo, . Faz sentido, certo? Afinal, no vácuo, . Na maioria dos casos, também admitimos o índice de refração do ar igual a 1.
Vimos que, quando a luz passa de um meio para o outro, a sua velocidade varia. Entretanto, a sua frequência permanece constante.
Assim, os únicos valores que variam de um meio para o outro são a velocidade e o comprimento de onda .
Como a velocidade da onda , a frequência e o comprimento de onda estão relacionados por
substituindo na fórmula do índice de refração , nós podemos reescrevê-la como função do comprimento de onda no vácuo e do comprimento de onda no material Dado por:
Pra finalizar, tem uma observação que é muito válida!
É muito importante você saber que o índice de refração não possui unidade de medida (adimensional).
Lei de Snell
Quando um raio de luz passa de um meio para um meio , os ângulos e estão relacionados com os índices de refração por:
A partir da Lei de Snell, podemos analisar algumas situações que podem nos ajudar bastante na hora de resolver as questões.
Vamos observar 3 casos:
:
Nesse caso, podemos observar que o raio refratado se aproxima do eixo normal. Logo:
:
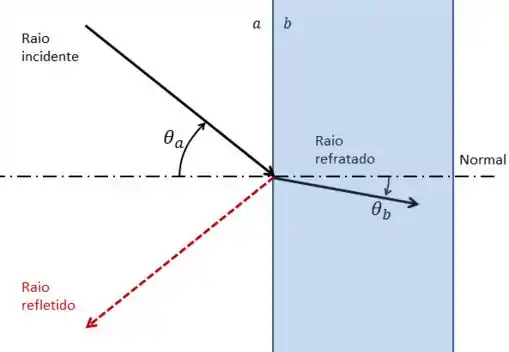
Nesse caso, podemos observar que o raio refratado se afasta do eixo normal. Logo:
:
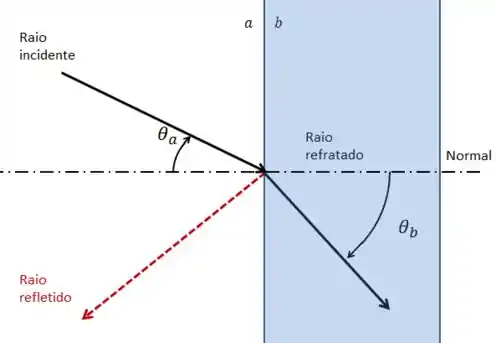
Nesse caso, podemos observar que o raio refratado não sofre desvio algum. Logo:
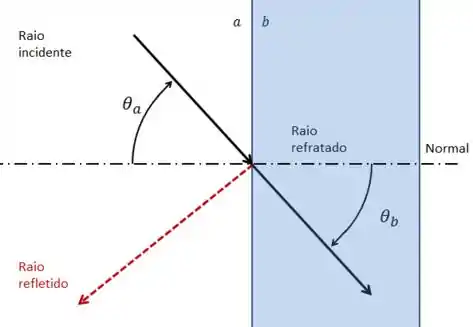
Agora conseguimos ter informações sobre a relação entre os índices de refração só de observar o problema.
Reflexão interna total
Vamos analisar um caso especial que acontece quando .
Vimos anteriormente que, neste caso, .
Onde é o ângulo de incidência e é o ângulo de refração.
Para explicar aonde vamos chegar, nós iremos nos basear na figura abaixo, analisando os raios 1, 2, 3 e 4.
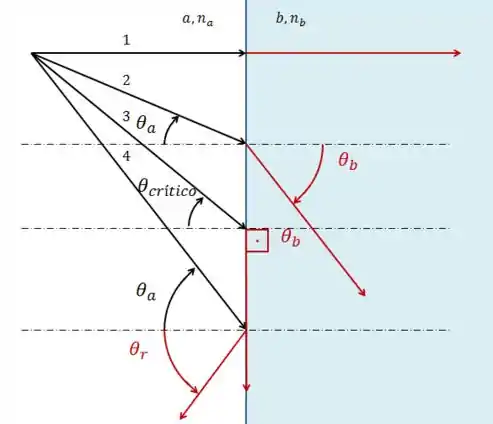
1. Inicialmente, os raios de incidência e refratado estão alinhados horizontalmente. Assim, os ângulos de incidência e de refração são nulos.
2. Agora, o ângulo aumenta e, como esperado, o ângulo é maior do que ele.
3. O ângulo aumenta até atingir o seu valor crítico. Neste ponto o ângulo vale e chamamos o ângulo de incidência de ângulo crítico .
Podemos determinar o valor de através da Lei de Snell, dada por:
Onde:
;
;
;
Logo:
4. Se o ângulo aumenta ainda mais, ultrapassando o valor , não ocorre mais refração e os raios luminosos passam a ser todos refletidos.
A esse fenômeno damos o nome de Reflexão interna total.
É por isso que, por exemplo, quando você vai à praia ver o por do sol, você vê o sol refletido na água, ao invés de conseguir ver o fundo do mar.
Você não precisa ir tão longe pra ver isso, basta encher um copo d’água. Comece olhando o copo de cima e você vai conseguir ver através da água. Depois vai abaixando a cabeça, aumentando o seu , a partir de certo momento você vai passar a ver o que a água está refletindo, sem nenhuma imagem refratada.
Lei de Snell
Reflexão interna total
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 63-64
A figura abaixo mostra um peixe e um banhista.
O banhista vê o peixe mais próximo do ponto ou do ponto ?
O peixe vê a cabeça do banhista mais próxima do ponto ou do ponto ?
Passo 1
O banhista vê o peixe mais próximo do ponto ou do ponto ?
Como a água possui índice de refração maior que o ar, o raio refratado se aproximará da normal quando passar do ar para água, sendo assim:
Logo, o banhista vê o peixe mais próximo do ponto .
Passo 2
O peixe vê a cabeça do banhista mais próxima do ponto ou do ponto ?
Como a água possui índice de refração maior que o ar, o raio refratado se afastará da normal quando passar da água para o ar, sendo assim:
Assim, o peixe vê o banhista mais próximo do ponto .
Resposta
O banhista vê o peixe mais próximo do ponto .
O peixe vê o banhista mais próximo do ponto .
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 74
Você olha para baixo, em direção a uma moeda que está no fundo de uma piscina de profundidade e índice de refração .
Como você observa a moeda com dois olhos, que interceptam raios luminosos diferentes provenientes da moeda, tem a impressão de que a moeda se encontra no lugar onda os prolongamentos dos raios interceptados se cruzam, a uma profundidade .
Supondo que os raios da figura acima não se desviam muito da vertical, mostre que .
(Sugestão: Use a aproximação, válida para ângulos pequenos, de que .)
Passo 1
Vamos começar fazendo uma análise gráfica do problema, mas para isso teremos que definir algumas coisas.
Na figura acima, e são os ângulos formados com a normal pelos raios incidentes e refratados, respectivamente. Além disso, é a distância entre o ponto em que os raios cruzam a interface entre os dois meios e o eixo central de onde se encontra a moeda.
Daqui podemos separar dois triângulos:
As tangentes de e são, respectivamente:
Considerando e suficientemente pequenos, podemos dizer que:
Passo 2
De acordo com a Lei de Snell, temos que:
Onde e, de acordo com o enunciado, , logo:
Fazendo as substituições das expressões que encontramos no Passo 1, teremos:
Organizando os termos, teremos, finalmente:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 74
Em um tanque, uma camada de água com de espessura flutua em uma camada de tetracloreto de carbono com de espessura.
Existe uma moeda no fundo do tanque. Você tem a impressão de que a moeda se encontra a que profundidade?
(Sugestão: Use o resultado e as suposições do problema anterior e faça um diagrama de raios da situação.)
Passo 1
Aqui usaremos o mesmo raciocínio usado no problema anterior, mas resolveremos o problema em duas partes.
Primeiro vamos considerar a interface água/tetracloreto. Nesse caso, a relação entre a profundidade real e a aparente no tetracloreto será dada por:
Substituindo os valores, teremos:
Passo 2
Vamos para a interface ar/água. Agora, o ponto onde a imagem se formou no Passo 1 servirá como um novo objeto que estará a uma distância da superfície, dada por:
Agora vamos aplicar a mesma equação que usamos anteriormente para calcular a profundidade aparente final.
Substituindo os valores, teremos: