Máquinas Térmicas
Produzido por Leonardo de BemTeoria
Fala aí! Bem vindo ao RespondeAí! Nessa página tentaremos entender o que são máquinas térmicas!
Uma máquina térmica é um aparato capaz de utilizar algum combustível para produzir calor (
Se isolarmos as peças de uma máquina térmica e tratarmos ela especialmente com olhar de um físico que estuda termodinâmica, podemos fazer o seguinte esquema:
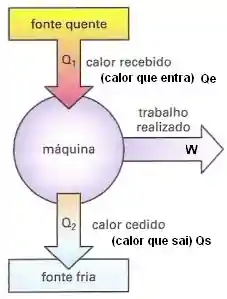
Voltando ao exemplo do motor, a gasolina provê a fonte quente, os pistões com o calor, movimentam as rodas e realizam trabalho, e o motor libera pelo escapamento o calor sobressalente.
Em um ciclo de uma máquina térmica podemos calcular o rendimento que ela possuí com a fórmula:
O trabalho do ciclo vale
E dessa forma podemos calcular o rendimento de uma máquina térmica.
O processo inverso também pode ser aplicado. As geladeiras por exemplo utilizam o trabalho gerado pela corrente elétrica no circuito, para manter ligado um compressor de ar. Dessa forma o gás fica comprimido e armazenado a uma alta pressão dentro da geladeira. Como o volume do sistema se mantém constante, a temperatura do gás diminui, e assim as geladeiras mantém os alimentos refrigerados.
Então as máquinas térmicas são equipamentos utilizados para realizar trabalho, e por isso em um motor temos que:
Porém no caso do refrigerador, temos que tirar o calor da fonte, por tanto precisamos que:
Exercício
Vamos ver como nosso Experts resolveriam um exercício do nosso tópico de Máquinas Térmicas e Refrigeradores:
Um gás ideal (
- O gás é monoatômico, diatômico ou poliatômica?
- Qual a eficiência da máquina?
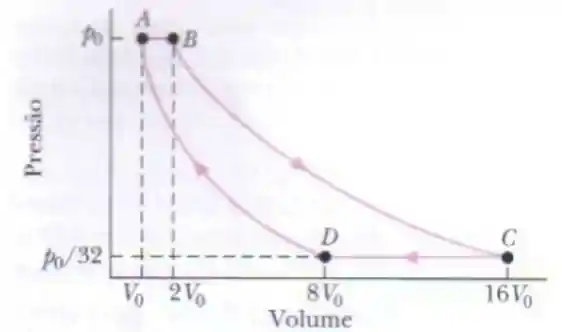
Exercício
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2. Rio de Janeiro: LTC , 2008. x-y 13
Quais são e , e o rendimento térmico da máquina térmica mostrada na figura?
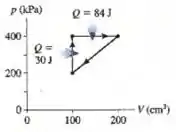
Passo 1
Quando estamos trabalhando com um ciclo, temos que o trabalho será a área interna ao ciclo, ou seja a área do triangulo:
Repare que temos que passar tudo para o sistema internacional!
Se liga que como o ciclo funciona no sentido horário, temos que o trabalho é positivo!
Passo 2
Agora que temos o trabalho, podemos determinar , pois sabemos que:
Substituindo os valores, temos:
Passo 3
O rendimento de uma máquina térmica pode ser determinado da seguinte forma:
É só substituir e correr pro abraço!
Show!
Resposta
;
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2. Rio de Janeiro: LTC , 2008,x-y 54
A figura mostra o ciclo de uma máquina térmica que usa gás com . A temperatura inicial é , e a máquina opera a ciclos por segundo.
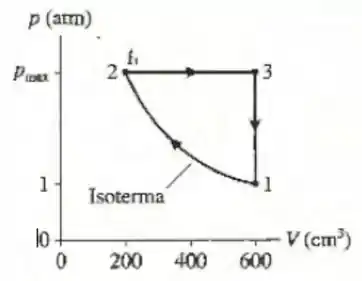
Qual é a potência de saída da máquina?
Qual é o rendimento térmico da máquina?
Passo 1
Para determinar a potência de saída da máquina, precisamos determinar o trabalho . Para determinar o trabalho, precisamos determinar e para cada um dos processos.
Para começar, precisamos determinar o número de mols do gás que temos, para isso, basta usar a clássica no ponto , pois conhecemos todos os dados para esse ponto, se liga:
Lembre-se de usar o !
agora que sabemos quantos mols estão envolvidos, podemos analisar cada processo do ciclo, começando pelo processo isotérmico:
Processo (isotérmico)
Processo (isobárico):
A gora que temos todas as informações do ciclo, podemos determinar e em cada processo, se liga no próximo passo!
Passo 2
Para o processo , temos:
Substituindo os valores, temos:
No processo isotérmico, temos:
Para o processo , temos:
Substituindo os valores, temos:
No processo isobárico, temos:
Pausa para calcular :
Então:
Voltando ao cálculo de , temos:
Para o processo , temos:
No processo isovolumétrico, temos:
Como já sabemos o valor de , , substituindo os valores, temos:
Agora que temos e para todos os processos, podemos determinar , basta somar!
Como temos que a máquina opera a ciclos por segundo, temos que a potência é dada por:
Passo 3
Para uma máquina térmica, temos que o rendimento é dado por:
Pelos cálculos, vemos que , substituindo, temos:
Resposta
Exercício Resolvido #3
UERJ – Lista para a 2ª Prova
A figura mostra um ciclo reversível percorrido por de um gás monoatômico ideal. O processo é uma expansão adiabática, com e. Para este ciclo, encontre:
A energia adicionada ao gás na forma de calor.
A energia liberada pelo gás na forma de calor.
O trabalho líquido realizado pelo gás
A eficiência do ciclo
Dados:
- gás monoatômico: , e
- pressão atmosférica
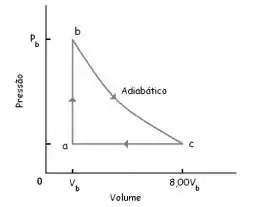
Passo 1
Bom galera, vamos utilizar uma série de relações importantes envolvendo gases pra resolver essa questão. Então apertem os cintos, lá vamos nós:
Bem, queremos saber aqui qual a quantidade de calor que adicionada ao ciclo pra que esse realize trabalho. Poderíamos analisar transformação por transformação e achar a contribuição de cada uma para o calor fornecido. Mas, vamos pensar um pouco sobre esse ciclo:
No trecho
Não há troca de calor aqui, pois é uma transformação adiabática (. O calor que foi fornecido ao ciclo não pode ter sido “injetado” aqui, né? (:
No trecho :
Bem, aqui há troca de calor. Porém, como o trabalho é negativo (o gás está se contraindo, diminuindo o seu volume), é de se esperar que esse seja o ponto de rejeição de calor para a fonte fria!
No trecho :
É aqui onde o calor tem que ser fornecido! Agora, precisamos calculá-lo:
Usando a primeira lei:
Perceba, pelo gráfico, que não há variação de volume nesse trecho! É uma transformação isovolumétrica, e isso quer dizer que . Logo:
Ok! Então basta calcularmos a variação de energia interna pra acharmos o trabalho. Lembrando que:
Temos o valor de e , mas precisamos descobrir o valor de .Vamos usar a equação geral dos gases para isso:
Vamos achar primeiro a temperatura do ponto , pois já temos o valor da pressão e volume desse ponto:
Agora vamos calcular . Pra isso, precisamos da pressão e do volume desse ponto, porém só temos o valor do volume. Mas perceba que a pressão daquele ponto é a mesma que a pressão do ponto !
Vamos descobrir então a pressão do ponto c. Como há uma transformação adiabática entre e , podemos achar a pressão de através da equação das transformações adiabáticas:
Como :
Então, vale:
Substituindo esse valor e os outros do enunciado na expressão que encontramos pro calor:
Conseguimos! Galera, não se assustem, esse tipo de questão é como um quebra cabeça. Aos poucos vamos descobrindo as informações de cada ponto do ciclo, e elas podem ser usadas nas outras opções da questão.
Passo 2
Agora queremos saber qual foi o calor rejeitado. Lembra da nossa análise? Vimos que o processo em que ocorrerá a liberação de calor para a fonte fria é o processo ! Vamos analisar esse processo com a primeira lei:
Podemos calcular :
Agora precisamos descobrir o valor de . Bom, uma forma de se descobrir isso é se lembrando que a variação total da energia interna em um ciclo é 0. Isso também nos diz que a soma das variações de cada trecho tem que ser igual a 0:
No trecho sabemos que :
Podemos calcular a variação e energia interna no trecho
Já foi calculado e vale:
A gente pode calcular facilmente, pois já temos a pressão e o volume do ponto c:
Logo:
Agora vamos descobrir :
Agora, sabendo o valor do trabalho e da variação de energia interna:
Passo 3
Essa é fácil! Depois de todo aquele trabalho, temos todas as informações pra resolver esse item! Vamos apenas usar a relação:
Outra que vamos resolver rapidamente já que já temos todas as informações necessárias. A eficiência de uma máquina térmica é:
Como:
Substituindo na expressão:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 270. x-y 32
Um gás ideal é a substância de trabalho em uma máquina térmica que descreve o ciclo mostrado na figura abaixo. Os processos e são reversíveis e adiabáticos. O gás é monoatômico, diatômico ou poliatômico? Qual é a eficiencia da máquina?
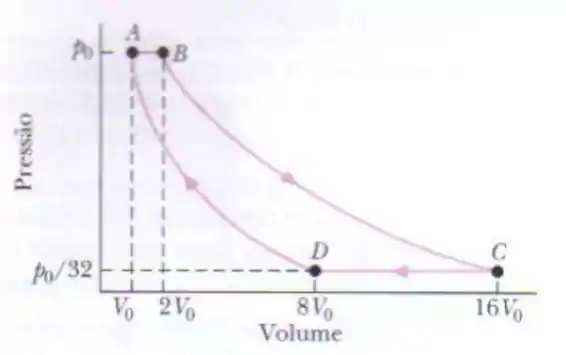
Passo 1
Temos que descobrir se o gás é monoatômico, diatômico ou poliatômico.
Para isso podemos analisar tanto o processo ou , nós vamos escolher analisar o processo .
Como o enunciado disse, é um processo adiabático. Então podemos usar a relação
Então no processo , temos que
O gráfico nos fornece o dado de pressão e volume nos estados e , substituindo na equação temos
Cortando os termos em cumun
Se lembrarmos da tabela que fizemos em uma das teorias anteriores, onde relacionamos com o grau de liberdade.
Assim, sabemos que se
Então o gás é monoatômico
Passo 2
Para calcular a eficiência da máquina vamos usar a fórmula que aprendemos
Como os processo e são adiabáticos isso significa que não há troca de calor nesses processo assim, sabemos que só há troca de calor nos processos e .
Sendo que no processo o sistema absorve energia, então é aqui que vamos calcular o , através da fórmula a seguir por ser um processo a pressão constante
Como o gás é monoatômico, temos que
Por “piviti-povotó” temos que
Como em , a pressão é constante, teremos:
Como :
Substituindo esse valores na fórmula de e o valor de e que temos no grágico, chegamos em
Pela equação geral dos gás temos que
Substituindo na equação de
O que vale
Passo 3
Agora no processo é onde o sistema vai liberar calor, sendo assim vamos calcular o
Assim como fizemos no processo , usando “piviti-povotó" temos que:
Como :
Assim,
Porém não sabemos o valor de , novamente vamos usar “piviti-povotó” para acharmos uma relação entre e , analisando o processo
Substituindo pelos valores do gráfico temos
Assim
Substituindo na equação de
Lembrando que
Chegaos em:
Passo 4
Agora que temos uma equação para e , vamos substituir na fórmula de rendimento da máquina térmica
Resposta
Monoatômico
Exercício Resolvido #5
UFRJ – 1ª Prova – 2015
Em uma máquina de Stirling idealizada o fluido de trabalho (considerado um gás ideal) realiza as seguintes etapas reversíveis:
: Uma expansão isotérmica do volume ao volume à temperatura .: Um resfriamento a volume constante, atingindo a temperatura .: Uma compressão isotérmica à temperatura , reduzindo o volume de a : Um aquecimento a volume constante, de forma que o gás retorne ao seu estado inicial.
Expresse suas respostas em termos de , , e , da constante dos gases , do calor específico molar a volume constante e do número de moles do fluido.
Esquematize o diagrama PV para este ciclo.
Calcule o trabalho realizado em cada etapa deste ciclo.
Calcule o calor transferido em cada etapa deste ciclo.
A eficiência da máquina.
Passo 1
Antes desenhar, vamos pensar um pouco:
Nos processos e , temos aquecimentos e resfriamentos à volume constante. Então sabemos que ali nós vamos desenhar retas paralelas ao eixo das pressões.
Os outros dois processos são transformações isotérmicas, então você já sabe que vão ter duas isotermas ali. Então, ligando os pontos com as isotermas e as transformações a volume constante, o gráfico ficará assim:
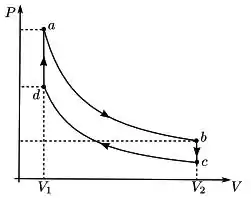
Passo 2
Onde existe realização de trabalho nesse ciclo? Onde há variação de volume! Então sabemos que não pode acontecer em e . Ali, como os volumes são constantes, o trabalho é igual à zero.
Logo, o trabalho ocorre nas transformações isotérmicas.
Vamos calcular primeiro o trabalho de :
O trabalho sempre é dado por:
Fazendo:
Logo:
No caso desse processo, , e :
Para o processo a coisa fica bem parecida, só que no caso . e :
Passo 3
Vamos analisar primeiro o processo
Como a temperatura é sempre a mesma, a variação de energia interna, que é uma função da temperatura, é nula. Isso sempre acontece: Quando a variação de temperatura é nula, a variação de energia interna também é. Então, pela primeira lei da termodinâmica:
Logo:
Aqui a gente calcule a troca de calor através da expressão básica do calor:
Podemos usar ou ou , dependendo do caso. Como a transformação é a volume constante, usamos . Então:
Aqui, novamente, por se tratar de uma transformação isotérmica:
De novo uma transformação isovolumétrica. Logo:
Passo 4
A eficiência será dada por:
O trabalho total será a soma dos trabalhos que a gente encontrou:
Já o calor que vem da fonte quente é dado por:
Logo:
Resposta
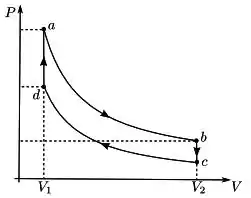
;
; ;
;
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 272. x-y 62
Um refrigerador ideal realiza de trabalho para remover em forma de calor do compartimento frio. Qual é o coeficiente de desempenho do refrigerador? Qual é a quantidade de energia em forma de calor liberada para a cozinha por ciclo?
Passo 1
O problema pede o coeficiente de desempenho de um refrigerador, como vimos na teoria a fórmula q vamos usar é
O enunciado nos fornece que
E
Como trabalhamos com módulo, o sinal não importa.
Assim,
Passo 2
Pela primeira lei da termodinâmica, temos o calor liberado será o calor retirado mais o trabalho, assim
Resposta
Exercício Resolvido #7
UFRJ – Prova Final – 2014.2
Um mol de gás ideal monoatômico é submetido ao ciclo mostrado na figura.
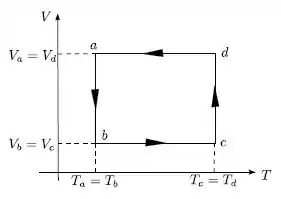
Desenhe o ciclo correspondente no plano (P.V) especificando o tipo de cada etapa.
Calcule o trabalho realizado (ou sofrido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Calcule o calor absorvido (ou cedido) pelo gás em cada etapa, em termos dos dados da figura e da constante universal dos gases .
Este ciclo corresponde a um motor ou a um refrigerador? Por quê?
Passo 1
Bom galera, pra desenhar isso ai é só você perceber qual é o processo que acontece em cada trecho:
: Processo isotérmico..
Processo isovolumétrico.
: Processo isotérmico..
Processo isovolumétrico. .
Então, o desenho ficará assim:
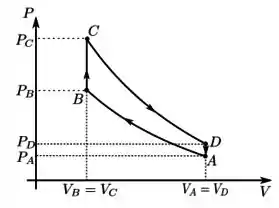
Passo 2
São 4 processos, mas dois deles acontecem a volume constantes. Então, o trabalho desses dois será igual à zero. Os outros dois processos são isotérmicos. Vamos lá:
: Processo isotérmico..:
O trabalho é dado por:
Como:
Então:
Show? Agora vamos substituir os valores que vemos no gráfico:
Como
É isso.
Processo isovolumétrico.
Como a gente viu:
: Processo isotérmico..:
Jogo rápido: Bem parecido com
Como
Processo isovolumétrico. .:
Como a gente viu:
Passo 3
Vamos lá:
: Processo isotérmico..:
Bom, como o processo é isotérmico, a variação da energia interna é nula e, pela primeira lei da termo, teremos:
Processo isovolumétrico.
O calor trocado aqui é o calor trocado a volume constante. Então você já sabe, vamos usar
Como o gás é monoatômico e se trata de um mol de gás:
Então:
: Processo isotérmico..
De novo, como é um processo isotérmico:
Processo isovolumétrico. .
Novamente, usando
Passo 4
Vamos olhar para o trabalho total. Se ele for negativo, é um refrigerador, se for positivo, é uma maquina térmica.
Então:
Como . O quociente acima vai dar um numero menor que 1. Então:
Mas, como , , então:
Show? Agora olhe o gráfico... é maior que . Então, o trabalho total é positivo.
Logo, o ciclo representa uma máquina térmica!!!
Resposta
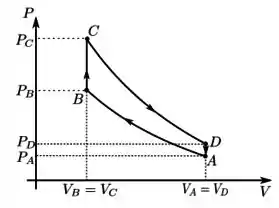
; ; ;
; ; ;
Logo, o ciclo representa uma máquina térmica!!!
Exercício Resolvido #8
PUC-RIO – 3ª Prova – 2010.2
Três mols de um gás ideal monoatômico passam pelo ciclo termodinâmico descrito na figura( isobárico, isotérmico e isocórico):
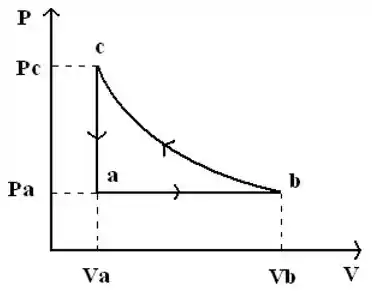
Dados , e , determine , e (tome e trabalhe com dois algarismos significativos).
Determine o trabalho realizado pelo sistema , o calor cedido ao sistema e a variação da energia interna para cada processo e preencha a tabela (justifique cada valor encontrado):

O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique
Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador), do ciclo.
Faça um gráfico do ciclo considerado.
Passo 1
Vamos primeiro reunir os dados fornecidos:
Analisando a figura, podemos dizer que:
Visto isso, podemos agora calcular o que foi pedido, vamos começar por
Passo 2
Para determinar , iremos utilizar a lei dos gases ideais:
Substituindo os valores que já temos:
Passo 3
Vamos agora determinar , para isso, iremos utilizar também a lei dos gases ideais:
Passo 4
Para determinar , usaremos, novamente a lei dos gases ideais:
Lembre-se que devemos utilizar apenas dois algarismos significativos!
Passo 5
Vamos analisar cada processo de uma vez, começando com :
Como temos um processo a pressão constante, podemos determinar o trabalho assim:
Para o calor trocado, sendo o processo a pressão constante, temos:
Para determinar a energia interna, podemos recorrer a primeira lei da termodinâmica:
Passo 6
Agora vamos analisar o processo :
Por ser um processo isotérmico, temos que a energia interna é zero!
Agora podemos calcular o trabalho realizado no processo:
substituindo por , temos:
Vamos agora substituir os valores conhecidos:
Pela primeira lei da termodinâmica, temos:
Passo 7
Finalmente, vamos analisar o processo :
Por ser um processo isovolumétrico, sabemos que o trabalho realizado é zero!
Vamos agora determinar o calor trocado no processo, que se dá a volume constante:
Pela primeira lei da termodinâmica, temos:
Agora é só completar a tabela!

Passo 8
Tendo em vista que o trabalho é negativo, e que o calor flui da fonte fria para a fonte quente, chegamos a conclusão de que se trata de um refrigerador.
Passo 9
Sabendo que se trata de um refrigerador, podemos calcular o coeficiente de desempenho:
Vamos primeiro calcular o trabalho realizado no ciclo:
Substituindo, temos:
Lembre-se que o calor retirado da fonte fria é :
Passo 10
Utilizando os dados obtidos no item , podemos montar o seguinte gráfico:
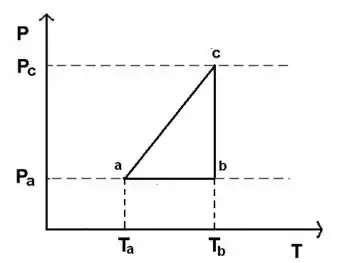
Resposta
; ;

Tendo em vista que o trabalho é negativo, e que o calor flui da fonte fria para a fonte quente, chegamos a conclusão de que se trata de um refrigerador.
