Ciclo de Carnot
Teoria
Bora aprender tudo sobre o Ciclo de Carnot e arrasar nas provas de termodinâmica!
O ciclo de carnot foi desenvolvido pelo engenheiro Sadi Carnot, em 1824, em seus estudos sobre as máquinas térmicas.
No ciclo de Carnot, um gás ideal passa por quatro transformações termodinâmicas, descritas a seguir:
- Expansão isotérmica - O gás sofre uma expansão, mantendo sua temperatura constante, e absorve calor
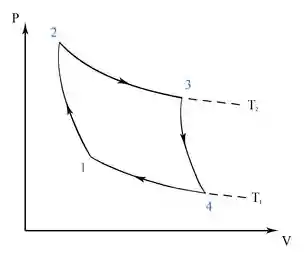
de uma fonte quente à temperatura (Representado pela curva 2-3 na figura abaixo); - Expansão adiabática - O gás se expande adiabaticamente, ou seja, sem ocorrer troca de calor com o meio, e por isso sua temperatura cai para um valor
(Representado pela curva 3-4 na figura); - Compressão isotérmica - O gás sofre uma compressão e libera calor
para uma fonte fria à tempratura (Representado pela curva 4-1 na figura); - Compressão adiabática - O gás retorna a condição inicial ao comprimir adiabaticamente, voltando para a tempratura
(Representado pela curva 1-2 na figura)
A principal característica do ciclo de Carnot e que faz ele ser tão famoso é que ele é o ciclo que tem o MAIOR rendimento possível entre duas temperaturas. Ou seja, para um mesmo intervalo de temperatura
E é daí que vem o Teorema de Carnot:
Rendimento no Ciclo de Carnot
No ciclo de Carnot, o rendimento é dado pela seguinte fórmula:
Onde:
é a eficiência do ciclo de Carnot; é a temperatura da fonte fria, que também pode ser chamada de , e; é a temperatura da fonte quente, que também pode ser chamada de .
Vamos fazer um exemplo aqui: Qual o rendimento de um ciclo de Carnot que opera entre as temperaturas
RESOLUÇÃO:
A temperatura da fonte fria é sempre menor que a da fonte quente: $T_F
Desse modo, o rendimento será:
Isso quer dizer que, entre
Maneiro, não é?
É isso que temos para te falar sobre o Ciclo de Carnot.
Vamos fazer um acordo? Você assiste esse vídeo aqui em seguida, só para revisar e fixar mais tudo o que vimos aqui e depois partiu exercícios. Estamos combinados?
Rendimento no Ciclo de Carnot
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 269. x-y 23
Uma máquina de Carnot tem uma eficiência de . Ela opera entre duas fontes de calor de temperatura constante cuja diferença de temperatura é . Qual é a temperatura da fonte fria e da fonte quente?
Passo 1
A eficiência de um ciclo de Carnot, é dada pela fórmula
Podemos reescrever isso, assim
Passo 2
Primeiro vamos descobrir a temperatura da fonte quente. Para descobrirmos a temperatura da fonte quente, vamos substituis os valor que temos
Lembre-se que a temperatura deve ser em kelvin, e que a variação em celsius é igual a variação em kelvin
Assim temos que
Passando para Celsius
Passo 3
Agora conseguimos facilmente descobrir o valor da temperatura da fonte fria, pois temos que
Substituindo o valor de
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 269. x-y 25
Uma máquina de Carnot opera entre e , absorvendo por ciclo na temperatura mais alta. Qual é a eficiência da máquina? Qual é o trabalho por ciclo que essa máquina é capaz de realizar?
Passo 1
Em questões de ciclo de Carnot vamos usar as fórmulas para calcular eficiência
E
Passo 2
Vamos usar a primeira fórmula, para calcular a eficiência do ciclo de Carnot, pois o enunciado nos forneceu as duas temperaturas
Lembre-se que a temperatura deve ser em kelvin
Passo 3
O problema nos diz que a máquina absorve na temperatura mais alta, isso é o calor absorvido pela fonte quente, logo
Sendo assim, agora vamos usar a segunda fómula que mostrei no “passo 1”
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 270. x-y 40
Qual deve ser o trabalho realizado por um refrigerador de Carnot para transferir em forma de calor de uma fonte de calor a para uma a , de uma fonte a para uma a , de uma fonte a para uma a e de uma fonte a para uma a ?
Passo 1
A questão quer que calculemos o trabalho de um ciclo de Carnot, sendo que temos apenas as temperaturas das fontes e o valor de
Então vamos achar uma relação entre elas, pela fórmula de eficiência de um refrigerador de Carnot
E
Igualando elas temos
Isolando o trabalho agora
Agora já temos a equação que vamos usar para resolver todos os itens.
Passo 2
Já vamos passar para kelvin, nesse item temos
Substituindo na fórmula que acabamos de encontrar, temos
Passo 3
Agora, temos
Substituindo na mesma fórmula, temos
Passo 4
Bom, vamos continuar fazenos o mesmo
Substituindo na mesma fórmula, temos
Passo 5
Por útimos, temos
Substituindo na mesma fórmula, temos
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 270. x-y 41
A figura abaixo mostra uma máquina de Carnot que trabalha entre as temperaturas e e alimenta um refrigerador de Carnot que trabalha entre as temperaturas e . Qual é a razão ?
Passo 1
Vamos relacionar a eficiência de uma máquina térmica de Carnot, para descobrir alguns dados dela como e e depois telacionar esses dados com o refrigerador e sua eficiência para descobrir o do refrigerador.
Para isso vamos usar
- Máquina térmica:
- Refrigerador
E lembrar que
Passo 2
Bom, vamos começar analisando a máquina térmica, dela queremos descobrir e para isso vamos achar sua eficiência, e depois relacionar o trabalho com
Para achar a eficiência é mole, certo? Temos as temperaturas das fontes, assim é só aplicar a fórmula
Lembrando que as temperaturas devem estar em kelvin,
Agora, para relacionar com o trabalho , temos
Assim,
Passo 3
Agora vamos analisar o refrigerador,
Primeiro calculando seu coeficiente de dempenho
Agora podemos relacionar o trabalho recebido com o do refrigerador
Pela fórmula a seguir descobrimos que
Como
Podemos escrever que
Substiuindo na fórmula acima
Passo 4
Vamos fazer a razão
Resposta
Exercício Resolvido #5
UFRJ – 1ª Prova -2015
A respeito de máquinas térmicas e refrigeradores assinale a alternativa INCORRETA.
Em um refrigerador sempre se joga mais calor na fonte quente do que se retirou da fria.
Um refrigerador perfeito (no qual o trabalho realizado é zero) pode ser pensado como uma máquina perfeita (para a qual a eficiência é de ) operando reversamente.
Pela segunda lei da termodinâmica podemos afirmar que não existem nem refrigeradores perfeitos nem máquinas perfeitas.
Quanto maior a diferença entre as temperaturas da fonte fria e da fonte quente tanto maior é a eficiência que uma máquina térmica pode ter.
Passo 1
Vamos analisar uma por uma:
Sim! Pois basta a gente lembrar daquela relação dos ciclos:
Ou seja, o calor da fonte quente é igual ao calor da fonte fria mais o trabalho. Você também pode pensar assim: A energia do trabalho que eu realizo pra retirar calor da fonte fria acaba sendo despejado junto, com o calor da fonte fria, na fonte quente.
Não! Se tivermos o trabalho igual à zero, a nossa relação vai ficar:
Agora imagine uma máquina térmica nessas condições....como podemos dizer que ela estará operando com uma eficiência de se ela não estará realizando nenhum trabalho? Não tem lógica, certo? Uma máquina térmica é muito eficiente quando recebe pouco calor e consegue converter quase todo esse calor em trabalho, não que despeja todo o calor que recebe na fonte fria (
Passo 2
Verdade. Essa é bem fácil, né? É, inclusive, um dos enunciados da segunda lei:
“É impossível construir um dispositivo que opere, segundo um ciclo, e que não produza outros efeitos, além da transferência de calor de um corpo frio para um corpo quente”
Verdade. Basta a gente se lembrar da fórmula:
Se , ou seja, se for muito maior, a eficiência tenderá a 1, ou seja,
Resposta
Exercício Resolvido #6
UERJ – Lista para 2ª
Para fazer gelo, um refrigerador, que é o inverso de uma máquina de Carnot, extrai sob a forma de calor, trabalhando a durante cada ciclo, com coeficiente de desempenho igual a . A temperatura ambiente .Determine:
Quanta energia por ciclo é fornecida na forma de calor para o ambiente.
Quanto trabalho por ciclo é necessário para funcionar o refrigerador.
Passo 1
Bom galera, nessa questão vamos usar basicamente o conceito de rendimento de um refrigerador. As relações que precisamos usar pra resolver essa questão são as seguintes:
Sendo que as últimas duas são aplicáveis apenas a ciclos de Carnot. Podemos nos perguntar, será que esse é um ciclo de Carnot? Posso usar essas relações? Como saber?
Fácil! Temos as temperaturas da fonte fria e da fonte quente e temos o coeficiente de rendimento. Vamos aplicar essas temperaturas na expressão do e se obtivermos o mesmo coeficiente, esse é um ciclo de Carnot!
Sendo:
Aplicando na fórmula:
Opa, então é mesmo um ciclo de Carnot!
Passo 2
Fica mais fácil começarmos pela , pois, conhecendo o trabalho, descobriremos o calor que é fornecido para o ambiente. Bom, sabemos o calor que é extraído do sistema, o , então podemos usar a relação abaixo pra achar o trabalho do ciclo:
Com:
Logo:
Passo 3
Agora vamos resolver
Queremos saber o calor que é liberado no ambiente, ou seja, o . Vamos usar a relação:
Com:
Logo: