![]()
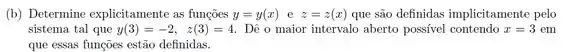
Passo 1
Equações que definem funções implicitamente são representadas na forma
Queremos determinar e como funções de , então
Passo 2
Primeiro vamos então jogar tudo para um lado só nessas equações:
Assim, temos
Beleza? Só substitui!
Passo 3
Agora, se a gente olhar a primeira equação, vemos que dá pra isolar o e já acha-lo como uma função de :
E substituindo isso na segunda equação, podemos achar em função de :
Passo 4
Beleza, e além disso, a gente sabe que
Substituindo nas equações que a gente encontrou:
Para isso dar , temos que ter então nosso
Fazendo a mesma coisa para a equação de :
E para isso dar , precisamos que nosso
Passo 5
Agora precisamos definir o intervalo que essas funções estão definidas.
Só recapitulando, nossas funções são
O intervalo em que elas estão definidas vai ser a interseção dos domínios dessas duas funções. Assim
Mas, como nosso intervalo tem que ser aberto e conter o ponto , temos que
É o maior intervalo aberto possível, contendo em que essas funções estão bem definidas.