P1 de Física 1 da UFV - 2022.1

Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.

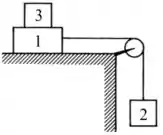
b) Determine a aceleração do bloco quando o bloco é removido subitamente de cima do bloco . Faça um diagrama de corpo livre para os blocos.

Questão 1) Um participante de desafios pretende chutar uma bola, inicialmente parada no chão de uma quadra, para acertar uma cesta de basquete, a uma altura do chão. Seja o módulo da velocidade imprimida à bola pelo chute, o ângulo entre o vetor velocidade inicial e a quadra e o módulo da aceleração gravitacional, determine:

a) O tempo decorrido entre o chute e o instante que a bola atinge a cesta (aro).

b) O vetor velocidade ao atingir o aro.

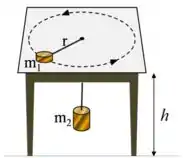
c) Com base nos seus resultados, a bola ao atingir o aro já passou pelo ponto mais alto da trajetória? Justifique sua resposta.

Questão 3). Um disco de metal de massa descreve uma circunferência horizontal de raio sobre uma mesa sem atrito, de altura , enquanto permanece ligado a um cilindro de massa pendurado por uma corda inextensível, de massa desprezível, que passa por um furo no centro da mesa, conforme representa a figura ao lado (sem escala). O disco () se move com velocidade constante, em módulo, para manter o cilindro () em repouso. A corda se rompe e o disco de massa é lançado horizontalmente, chegando ao solo depois de percorrer uma distância horizontal . Sabendo que e que o alcance é o dobro da altura da mesa , determine o raio da circunferência descrita pelo disco antes da corda se romper. Escreva sua resposta em termos de . 🤔

Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.

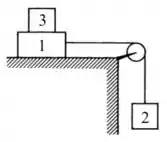
a) Determine a massa mínima do bloco () para impedir que o bloco deslize. Faça um diagrama de corpo livre para os três blocos.