Questão 1) Um participante de desafios pretende chutar uma bola, inicialmente parada no chão de uma quadra, para acertar uma cesta de basquete, a uma altura do chão. Seja o módulo da velocidade imprimida à bola pelo chute, o ângulo entre o vetor velocidade inicial e a quadra e o módulo da aceleração gravitacional, determine:

a) O tempo decorrido entre o chute e o instante que a bola atinge a cesta (aro).

b) O vetor velocidade ao atingir o aro.

c) Com base nos seus resultados, a bola ao atingir o aro já passou pelo ponto mais alto da trajetória? Justifique sua resposta.

Antes de começar a responder as perguntas, temos que ter em mente uma coisa muito importante!

Estamos trabalhando com um lançamento oblíquo já que um chute faz com que a bola tenha um movimento parabólico. Nesses problemas temos dois tipos de movimentos, o movimento horizontal e o movimento vertical. O movimento horizontal é caracterizado por ser um movimento uniforme e o movimento vertical por ser um movimento acelerado.

Não sabemos qual é a distância horizontal entre a bola e a cesta, então vamos atribuir uma variável a ela.

Respondendo a primeira pergunta “qual é o tempo que a bola leva para chegar à cesta?”.

Se horizontalmente o movimento é uniforme, podemos descrever seu movimento pela formula da velocidade, não é?

Qual é a componente do vetor ? Desmembrando o vetor, vemos que

Substituindo na formula da velocidade, temos

Isolando

Então vemos que o tempo que a bola demora a atingir a cesta depende da distância horizontal entre elas, da magnitude do vetor velocidade inicial e do ângulo entre o vetor e o plano horizontal!

Entendeu? Bora pra próxima!

A segunda pergunta é: qual é o vetor velocidade da bola ao atingir o aro?

Dado que o movimento horizontal é uniforme, a componente do vetor velocidade sempre será a mesma em todo o trajeto até a cesta.

Já a componente do vetor velocidade não é uniforme pois sofre a ação da aceleração gravitacional . As equações que descreve esse movimento são dadas no nosso caso por

Usamos o sinal de menos pois a aceleração gravitacional aponta para baixo.

Vamos usar a primeira equação. Substituindo por

Como é igual a , então

Tirando a raiz dos dois lados podemos eliminar o expoente de

Com isso, podemos dizer que a felicidade final é dada por , ou seja

Será que é isso mesmo? 🤔🤔

Para saber se a resposta anterior está correta, temos que pensar em uma coisa que é justamente a terceira pergunta que temos que responder.

ao atingir o aro, a bola já passou pelo seu ponto mais alto da trajetória?

Como é a trajetória da bola antes de atingir seu ponto máximo? A sua altura aumenta de forma amortecida, não é? Ou seja

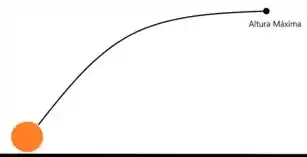
Nesse intervalo, pra onde aponta a componente do vetor velocidade? Se o vetor velocidade é tangente à trajetória então um vetor tangente a essa trajetória aponta para cima, correto?

Mas como vamos fazer uma cesta se a bola está indo para cima?? 🤔🤔

Para fazermos a cesta, a bola deve cair dentro dela, ou seja, o movimento em deve apontar para baixo.

E isso só acontece depois que a bola atinge sua altura máxima, portanto a resposta é “SIM! ao atingir o aro, a bola já passou pelo seu ponto mais alto da trajetória”.

Logo, a componente de deve apontar para baixo, ou seja, deve ser negativa!

Logo a resposta correta para o item anterior é

Agora sim! Entendeu tudo?

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí