Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.
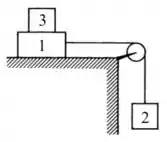
a) Determine a massa mínima do bloco () para impedir que o bloco deslize. Faça um diagrama de corpo livre para os três blocos.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão temos três blocos onde o bloco , de massa , está sob uma mesa, o bloco , de massa , está suspenso no ar e está ligado ao bloco através de uma corda de massa desprezível que passa por uma polia sem atrito e por fim o bloco , de massa , está sob o bloco . Podemos ver isso na imagem do enunciado.
Sabendo que e são os coeficientes de atrito estático e cinético qual deve ser a massa do bloco para que o bloco não deslize sobre a mesa?
Tem ideia de como fazer isso? 🤔🤔
Antes de tudo, vamos relembrar algumas equações importantes!
A força de atrito que um objeto sofre sob o efeito contrario ao movimento é
Onde é a força normal do objeto.
E um objeto suspenso no ar exerce uma força que chamamos de força peso
Com isso, podemos começar os cálculos do nosso problema!
Bora? 😁
Passo 2
Para o bloco não deslizar sobre a mesa, temos que ter um sistema em equilíbrio.
Primeiro vamos desenhar as forças que atuam nos blocos.
No bloco temos a força peso , a força normal , a força de atrito e a tração da corda .
No bloco temos a força peso e a tração da corda .
E no bloco temos apenas a força peso e a força normal .
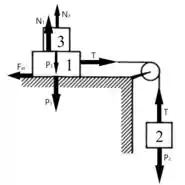
As forças de tração da corda se cancelam já que a polia não tem atrito.
O sistema está em equilíbrio, então todas as forças se cancelam! As forças peso e se cancelam com as forças e , respectivamente.
Perceba que a força peso do bloco , indiretamente, exerce uma força horizontal para a direita no bloco e se o bloco está parado, logo essa força deve ser cancelada de alguma forma.
A força que faz esse cancelamento é justamente a força de atrito entre o bloco e a mesa.
Assim, podemos dizer que
Entendeu? 👀
Passo 3
Mas o que é e ?
A força de atrito é dada como como vemos no passo 1.
Mas precisamos adaptar esse formula ao nosso problema, não é?
O bloco não desliza, então temos que considerar o coeficiente estático de atrito no lugar de .
E a força normal? Temos que considerar apensas o bloco ? Não né.
Os blocos e estão empilhados em cima da mesa, então temos que considerar as duas forças normais na conta, ou seja
A força normal é a força contraria à força peso, ou seja
Para o bloco de massa , temos
Já para o bloco de massa
Substituindo esses valores em
Entendeu essa parte? 🤩
Passo 4
Já a força peso do bloco é dado mais facilmente por
Igualando e , temos
Simplificando dos dois lados, vamos obter
Isolando em um lado da equação
Logo, essa é a equação que relaciona , , e . Faz sentido?
Se for muito pequeno, menor será o atrito e ou deverá ser muito grande para equilibrar o sistema.
A mesma coisa se for muito gande... ou também deverá ser muito grande.
Já se for pequeno e grande, deverá compensar a falta de peso em .
Então, sim! Esse resultado faz sentido!
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
a)