Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.

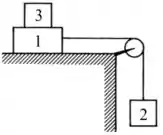
b) Determine a aceleração do bloco quando o bloco é removido subitamente de cima do bloco . Faça um diagrama de corpo livre para os blocos.

Quais são as forças que agem sobre o bloco ?

Certamente a força peso , a força normal , o bloco se movimenta, então temos a ação da força de atrito também e como os blocos e estão ligados por uma corda e o bloco está suspenso, há uma força tensionando a corda que chamamos de tração .

E para o bloco ?

Para ele tem bem menos vetores. Um deles é a força peso e o outro é a força que o bloco faz na corda, ou seja, a mesma tração do bloco anterior.

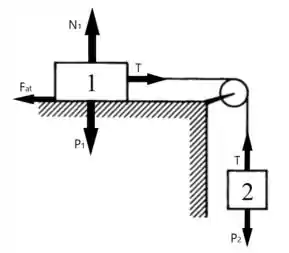
Concorda? 😎

Sabemos que a força é má, ou seja, . Então quando tiramos o bloco do sistema e ele começa a se mover, o sistema estará aplicando uma força.

Como o sistema é formado pelos blocos e e como eles se movimentam na mesma velocidade, então

Mas o que é esse ? Perceba que de um lado da corda o bloco puxa com a força e do outro lado o atrito entre o bloco e a mesa geram uma força contrária dada por .

e não se cancelam como antes, então essa diferença entre elas geram justamente a força , ou seja

A força de atrito é dada pelo produto do coeficiente de atrito e a normal, ou seja

(usamos pois o bloco está se movendo)

Se a normal é a força contraria a força peso, então

E é a força peso do bloco dada por

Tranquilo até aqui? 👀

Se , fazendo as substituições necessárias, temos

Isolando em um lado da igualdade, temos

Simplificando a equação, temos

Faz sentido? 🤔

Se for muito grande e pequeno, então vai ser alto. Mas se for grande e for pequeno, será baixo já que a força de atrito será maior.

Então essa resposta faz sentido sim! 😁

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍