P2 de Física 1 da UNICAMP - 2015.1 Diurno
Física 1 - UNICAMP
Uma conta de massa escorrega com atrito desprezível ao longo do arame mostrado na figura abaixo. Se a altura e a velocidade iniciais da conta são conhecidas, existem pelo menos dois métodos para encontrarmos o módulo da velocidade final da conta para uma dada altura final. São eles:
Resolver as leis de Newton para todas as forças do sistema;
Aplicar a conservação da Energia Mecânica.
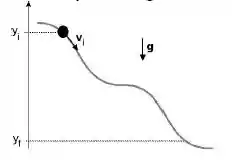
Podemos então afirmar que:
O grau de dificuldade é o mesmo para os dois métodos, já que é necessário o conhecimento das forças que atuam na conta em ambos os casos.
É mais fácil resolver o problema utilizando Conservação da Energia Mecânica porque o movimento da conta depende da força aplicada pelo arame.
Como a velocidade da conta na altura final não depende da força aplicada pelo arame, então é mais fácil usar as Leis de Newton.
É mais fácil resolver o problema utilizando as Leis de Newton porque basta conhecer a aceleração para encontrarmos a velocidade.
É mais fácil resolver o problema utilizando Conservação de Energia Mecânica porque o módulo da velocidade na altura final não depende da força aplicada pelo arame.
Ver solução completaUm bloco de massa desliza sem velocidade inicial ao longo de uma rampa sem atrito a partir de uma altura e colide com um bloco de massa , inicialmente em repouso. Após a colisão, o bloco desliza em uma região com coeficiente de atrito cinético até finalmente parar após percorrer uma distância . Qual é o valor de se a colisão for:
elástica?
perfeitamente inelástica?
Dica: Este exercício fica mais fácil de resolver se você deixar para substituir os valores das várias grandezas apenas perto do final, e só então fazer as contas.

Uma moeda de massa é abandonada a partir do repouso do topo do edifício Itália, em São Paulo, que tem aproximadamente metros de altura. A moeda atinge a velocidade limite de antes de atingir o chão.
O trabalho da força de arraste durante todo o trajeto de queda da moeda é de:
Ver solução completa
Se a energia potencial relacionada a uma força aplicada em um bloco pode ser expressa por , onde e são constantes, podemos dizer que a força tem a forma:
constante
nenhuma das outras respostas.
Ver solução completaUma moeda de massa é abandonada a partir do repouso do topo do edifício Itália, em São Paulo, que tem aproximadamente metros de altura. A moeda atinge a velocidade limite de antes de atingir o chão.
Após atingir a velocidade limite, o módulo da potência dissipada pela força de arraste do ar é:
Ver solução completa
Uma força constante de módulo age sobre um bloco de massa , que pode se mover sobre uma superfície sem atrito. Assinale a alternativa incorreta.
se o bloco realiza um percurso fechado, o trabalho da força é nulo.
o trabalho realizado pela força pode ser negativo, dependendo do ângulo entre os sentidos de e o do movimento.
A força é conservativa se a direção do movimento for a mesma da direção de aplicação da força.
É possível definir uma energia potencial relacionada à força .
O trabalho da força é igual à variação da energia cinética do bloco somente se esta for a força resultante aplicada ao bloco.
Ver solução completaNa figura abaixo é apresentado o comportamento de uma força aplicada em um bloco em função da sua posição. Se o bloco se encontra em repouso instantâneo no ponto , é possível afirmar que:
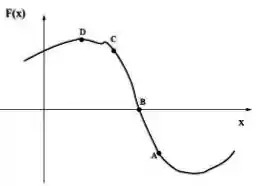
Ele volta a estar em repouso nas proximidades do ponto .
Ele volta a estar em repouso nas proximidades do ponto .
Ele terá sua maior energia cinética no ponto .
Ele se deslocará na direção de positivo.
A energia potencial apresenta um máximo no ponto .
Ver solução completaNa figura abaixo é apresentado o comportamento de uma curva de energia potencial (cuja unidade é o ) como função da posição. Além disso, quando . Se uma partícula se encontra em repouso no único ponto de equilíbrio estável, qual energia mínima deve ser fornecida para que a partícula descreva um movimento não confinado?
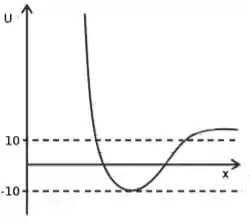
Ver solução completa
Em uma barra uniforme de comprimento e massa , fixa-se uma partícula de massa em uma das extremidades, e outra massa na outra extremidade. O centro de massa desta distribuição encontra-se a que distância da partícula de massa ?
Ver solução completa
Duas partículas de mesma massa estão ligadas por uma corda de massa desprezível. Uma das partículas é lançada para cima com velocidade , enquanto a outra está em repouso no chão. É correto afirmar sobre o centro de massa desta distribuição:
descreve uma trajetória com aceleração para baixo, mesmo enquanto uma das massas ainda está em contato com o chão.
descreve uma trajetória com aceleração para baixo a partir do momento que as duas bolas perdem o contato com o chão, com exceção dos momentos em que a corda está tensionada.
descreve uma trajetória com aceleração para baixo a partir do momento que as duas bolas perdem o contato com o chão.
descreve uma trajetória com aceleração menor que , para baixo a partir do momento que as duas bolas perdem o contato com o chão.
não é possível calcular a aceleração do centro de massa sem descrever a força de tensão da corda.
Ver solução completaEm um sistema de partículas em que não há forças externas é correto afirmar que:
Sempre há conservação de energia mecânica do sistema
Sempre há conservação do momento linear total do sistema
Sempre há conservação da Energia Cinética total do sistema
Forças dissipativas internas podem reduzir o momento linear total
Pode haver transferência do momento linear para energia cinética, através da ação de forças conservativas.
Ver solução completaUm astronauta está flutuando no espaço, segurando uma caixa de massa . A massa do astronauta juntamente com todo seu equipamento (excetuando a caixa) é de . Ele lança a caixa a uma velocidade de para a direita. Após o lançamento, sua velocidade será de:
para a esquerda
para a esquerda
para a esquerda
m/s para a esquerda
m/s para a esquerda
Ver solução completaEm uma colisão elástica, uma partícula de e velocidade atinge outra partícula de massa , e que seguia na mesma direção com velocidade de . As velocidades finais das partículas são respectivamente:
não há como calcular as velocidades sem informações sobre se o momento linear é conservado.
Ver solução completaUma bala é atirada a uma velocidade de em um bloco de madeira, atravessando-o e saindo a uma velocidade de sem desviar sua trajetória. Se a massa da bala é de e a do bloco é de , qual a velocidade final do bloco?
Ver solução completa
Duas partículas de mesma massa e traçando trajetórias ortogonais colidem, e seguem grudadas após a colisão. O ângulo que as partículas grudadas fazem com a direção original da primeira partícula é de , conforme desenho abaixo. Qual a razão entre as velocidades iniciais das partículas?
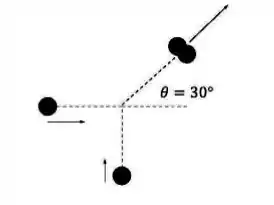
Ver solução completa