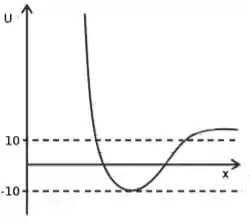
Na figura abaixo é apresentado o comportamento de uma curva de energia potencial (cuja unidade é o ) como função da posição. Além disso, quando . Se uma partícula se encontra em repouso no único ponto de equilíbrio estável, qual energia mínima deve ser fornecida para que a partícula descreva um movimento não confinado?
Passo 1
Bem, primeiro temos que encontrar o ponto de equilíbrio estável. Então vamos imaginar uma bolinha es duas seguintes situações:

As duas situações são de equilíbrio, porém em uma temos o equilíbrio estável, onde podemos dar uma energia na bolinha e ela tende a voltar a posição inicial. E a outra situação é de equilíbrio instável, que apesar do equilíbrio qualquer energia vai tirar a bolinha do equilíbrio par sempre.
A primeira imagem é a do equilíbrio estável e por isso no gráfico temos uma posição como essa que a quando temos energia potencial igual a .
O gráfico e o enunciado mostram que quando o sistema está no infinito .
Então essa é a posição que vai tirar nosso sistema de equilíbrio, se estamos em e queremos chegar em quanto de energia deve ser fornecido a partícula?
Essa é a energia necessária para fazer a partícula sair do estado confinado.
Resposta
Alternativa