Uma conta de massa escorrega com atrito desprezível ao longo do arame mostrado na figura abaixo. Se a altura e a velocidade iniciais da conta são conhecidas, existem pelo menos dois métodos para encontrarmos o módulo da velocidade final da conta para uma dada altura final. São eles:

Resolver as leis de Newton para todas as forças do sistema;

Aplicar a conservação da Energia Mecânica.

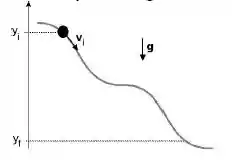
Podemos então afirmar que:

O grau de dificuldade é o mesmo para os dois métodos, já que é necessário o conhecimento das forças que atuam na conta em ambos os casos.

É mais fácil resolver o problema utilizando Conservação da Energia Mecânica porque o movimento da conta depende da força aplicada pelo arame.

Como a velocidade da conta na altura final não depende da força aplicada pelo arame, então é mais fácil usar as Leis de Newton.

É mais fácil resolver o problema utilizando as Leis de Newton porque basta conhecer a aceleração para encontrarmos a velocidade.

É mais fácil resolver o problema utilizando Conservação de Energia Mecânica porque o módulo da velocidade na altura final não depende da força aplicada pelo arame.

Analisando cada alternativa fica mais tranquilo da gente identificar qual é a certa e qual é a errada, além de sabermos justificar todas as alternativas. Sendo assim ...

1. O grau de dificuldade entre as duas alternativas é totalmente diferente. Enquanto pelo método de conservação de energia é necessário saber apenas as alturas do início e do final, o outro método precisa saber como as forças vão variar de acordo com o tempo, pois as leis de Newton relaciona a força em cada momento com a aceleração da partícula:

Já a conservação de energia, vai estudar apenas o estado inicial e final, já que não tem atrito.

Então sabendo a altura inicial e final e a velocidade inicial, você consegue descobrir a velocidade final.

2. É realmente mais fácil resolver por energia mecânica, porém não tem relação com a força aplicada pelo arame, e sim com as alturas do início e final do problema como terminamos de ver;
3. As leis de Newton não são o melhor jeito, já que as forças variam com o tempo e não sabemos como calcula-las;
4. O problema tá nesse “basta” ai. Descobrir a aceleração nesse problema é muito difícil, já que as forças que atuam no corpo mudam com o passar do tempo;
5. Essa tá muito certa, é mais fácil por energia mecânica e não depende da força aplicada, apenas da altura inicial e final.