P2 de Física 2- FIS1041 da PUCRIO - 2011.2

Um fio muito longo é feito juntando-se (no ponto B) dois fios com densidades lineares diferentes e . A figura abaixo mostra uma porção do fio, centrada na junção. O fio é esticado sob uma tensão .

1. No instante , é produzido um pequeno pulso transversal, localizado no ponto A. Considere as distâncias indicadas na figura. Em que instante de tempo o pulso atinge o ponto C?
2. Parte do pulso do item (a) é refletida na junção (ponto B). Determine o instante de tempo em que essa parte do pulso volta ao ponto A?

Em uma corda muito longa se propagam duas ondas progressivas harmônicas dadas por e .

3. Some as duas ondas e obtenha a resultante da sua superposição.
4. Caracterize o tipo de interferência resultante (construtiva ou destrutiva, total ou parcial), para cada um dos seguintes valores de e .

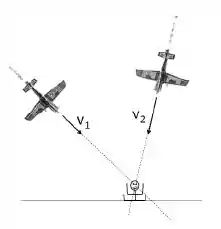
Na competição aérea Red Bull, um avião voa a velocidade constante se aproximando em linha reta de um espectador sentado no chão fora da área de segurança. O motor do avião produz um som de frequência . Considere que o ar está em repouso em relação ao solo.

1. Calcule a frequência do som ouvido pelo espectador.
2. Simultaneamente, um segundo avião, com o mesmo motor que o primeiro produzindo um som de , também se aproxima do espectador, em linha reta (ver figura), a velocidade constante . Da superposição de ambos os sons percebidos pelo espectador, ele ouve 2 batimentos por segundo. Determine a velocidade .

Seja uma onda sonora harmônica, com frequência igual a e intensidade . A velocidade do som no ar é e a densidade do ar é .Dado:

1. Calcule o nível sonoro, a amplitude do deslocamento e o valor máximo da variação de pressão.
2. Para essa onda se propagando na direção horizontal, no sentido negativo do eixo x, escreva a função que descreve a onda de deslocamento , especificando todos os valores numéricos, dado que em a camada de ar em está deslocada por , e se movimentando com a velocidade positiva.

O modo fundamental de vibração de uma corda de violão (fixa nas extremidades) é descrito por .

1. Determine o comprimento de onda, a frequência, e a amplitude máxima de vibração.
2. Determine o comprimento dessa corda.

Perto da corda do violão que vibra no modo fundamental, encontram-se vários tubos de diferentes comprimentos, de valores entre e , abertos em ambas as extremidades. Alguns deles entram em ressonância devido ao som produzido pela corda do violão. Considere .

3. Faça um desenho esquemático da onda estacionária de deslocamento, para cada um dos 3 primeiros harmônicos num desses tubos, e determine a relação entre o comprimento do tubo e o comprimento de onda. A partir dessas relações, ache a expressão geral para a frequência do enésimo harmônico, em função de e .
4. Determine os possíveis valores do comprimento daqueles tubos que ressoam com a frequência fundamental da corda do violão.