P2 de Física 2- FIS1041 da PUCRIO - 2012.2

Um sistema consiste de duas fontes emitindo, em fase, som com a mesma frequência angular dada por . A primeira fonte encontra-se a uma distância do observador, emite com potencia , e chega na posição do observador com amplitude . A fonte se encontra à distância do observador com a potencia vezes maior do que a primeira fonte. Considere que .

Calcule a razão entre as amplitudes e das ondas e, ao chegarem separadamente ao observador.

Calcule a diferença de fase entre as ondas na posição do observador e diga qual o tipo de interferência observado.

Uma corda de violino tem comprimento de e está afinada na nota sol, .

A que distância da extremidade se deve apertar a corda para que soe como um lá, ?

Se o violinista quisesse afinar essa mesma corda em lá, que variação relativa de tração ele deveria fornecer?

Uma sirene, que emite um som com frequência de , se afasta de um observador parado com uma velocidade . Mais afastado, há um carro com detector, que se movimenta no mesmo sentido da sirene com velocidade de (ver figura). (Considere que o ar está parado e que a velocidade do som no ar é .

Calcule a frequência do som que o observador escuta vindo diretamente da sirene.

Determine a frequência do som recebido pelo detector.

Um pulso numa corda é descrito pela função e um segundo pulso, na mesma corda, é descrito por onde são dados em e em segundos.

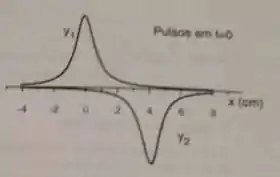
Em que direção cada pulso se propaga? Calcule a velocidade de cada pulso.

Determine em que instante os dois pulsos se cancelam totalmente.

Determine em que ponto os pulsos sempre se cancelam.

Uma corda submetida a uma tensão de e fixa nas duas extremidades, oscila num padrão de onda estacionária correspondente ao terceiro modo normal de vibração. Uma das extremidades da corda encontra-se em e o deslocamento da corda é dado por:

(Sistema Internacional de Unidades)

Determine o comprimento da corda.

Calcule a velocidade das ondas na corda e a massa total da corda.

Obtenha a expressão da velocidade transversal das partículas da corda em função de e . Calcule essas velocidades em , nas posições .

Faça um desenho da corda em , indicando as posições dos nós e colocando os vetores velocidade nas posições e.

Desenhe a corda depois de decorrido um quarto de período .