Uma corda submetida a uma tensão de e fixa nas duas extremidades, oscila num padrão de onda estacionária correspondente ao terceiro modo normal de vibração. Uma das extremidades da corda encontra-se em e o deslocamento da corda é dado por:
(Sistema Internacional de Unidades)
Determine o comprimento da corda.
Calcule a velocidade das ondas na corda e a massa total da corda.
Obtenha a expressão da velocidade transversal das partículas da corda em função de e . Calcule essas velocidades em , nas posições .
Faça um desenho da corda em , indicando as posições dos nós e colocando os vetores velocidade nas posições e.
Desenhe a corda depois de decorrido um quarto de período .
Passo 1
Para determinar o tamanho da corda, precisamos atentar para um detalhe dado no enunciado, temos a informação de que a corda oscila em um padrão estacionário correspondente ao terceiro modo de vibração, temos então:

Ou seja, temos pontos (nós) onde a função será igual a zero, ou seja, temos que esses pontos ocorrem quando é igual a . Ou seja, deve valer e para cada um dos nós, sendo no primeiro e no último!
Então, para determinar o comprimento da corda, basta calcular quanto vale para que seja igual a !
Passo 2
Da função , podemos extrair algumas informações, se liga! Temos que o número de onda , pois essa é a constante que multiplica , pela definição de , temos:
Além disso, temos que , da definição de , temos:
Agora é só lembrar de e correr pro abraço!
Para determinar a massa, precisamos lembrar da seguinte relação:
Onde é a densidade linear da corda, vamos primeiro determinar seu valor!
Para determinar a massa, basta fazer:
Passo 3
Para determinar a velocidade transversal, vamos precisar derivar a função , que temos, se liga!
Agora é só calcular a velocidade nos pontos pedidos, simbora! Precisamos calcular essas velocidades em , nas posições .
Para , temos:
- Para , temos:
- Para , temos:
- Para , temos:
Passo 4
Para fazer o desenho da corda, precisamos relembrar de algumas coisas. Primeiro, temos que a corda oscila no terceiro modo de oscilação, ou seja, temos uma configuração com nós, sendo que são as extremidades. Além disso, para , temos que para todos os valores de ,ou seja, a corda está esticada sobre o eixo . Para expressar os vetores, basta notar o sentido da velocidade que calculamos no item anterior. Como temos que o eixo aponta para cima, teremos então o seguinte desenho:
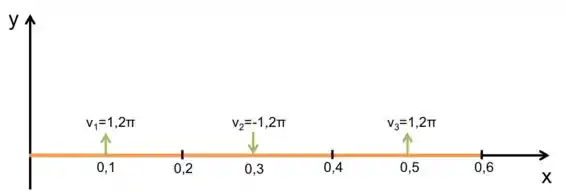
Onde os nós estão indicados por traços pretos no eixo , correspondendo aos pontos , , e , e os vetores velocidade estão destacados em verde.
Passo 5
Para poder desenhar a corda, precisamos primeiro determinar o instante de tempo indicado, temos que , podemos determinar o período pois sabemos a frequência , se liga!
Para , temos:
Substituindo em , temos:
Agora é só plotar esse gráfico, teremos algo semelhante a isso:
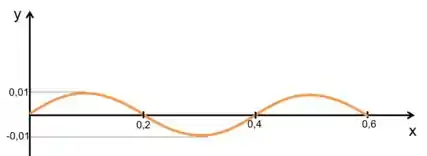
Resposta
;
-
-
-
Ver desenho acima.
Ver desenho acima.