P2 de Física 2- FIS1041 da PUCRIO - 2013.2

A função de onda para uma onda progressiva em uma corda esticada é ( em unidades do SI):

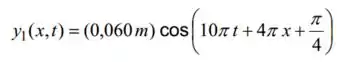
Suponha que a corda possui uma massa por unidade de comprimento de

1. Obtenha o comprimento de onda, a velocidade e o sentido de propagação da onda.
2. Obtenha o valor máximo de velocidade transversal da corda. Para a posição , em que instantes esse valor máximo ocorre?( Dê os dois primeiros, para
3. Determine a tensão na corda e a potência média transmitida por esta onda.
4. Escreva a função de onda que sobreposta a uma função produza uma onda estacionária. Obtenha a função de onda estacionária.
5. Determine as duas primeiras posições para os dois primeiros nós da onda estacionária gerada.

1. A figura abaixo representa um carro que se aproxima de uma parede que reflete o som. O carro buzina com frequência . Um observador em repouso na posição indicada na figura detecta batimentos com frequência de Considere a velocidade do som

1. Obtenha a expressão para a frequência de batimento em função da frequência da buzina e da razão entre as velocidades do carro e do som,
2. Calcule a velocidade do carro.

1. Na figura abaixo, dois alto-falantes e estão separados por uma distância em um palco ao ar livre. Durante o teste do som, os dois alto-falantes emitem, em fase, sons com comprimento de onda
2. Um ouvinte encontra-se inicialmente sobre o eixo a do alto falante e pode se deslocar sobre esse eixo em direção a Considere apenas os valores de .

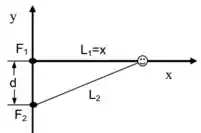
1. Encontre as duas posições do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva).
2. Em que posição(ões) do ouvinte a intensidade sonora passa por uma máximo(interferência construtiva)?

1. Um tubo de comprimento é fechado em uma extremidade Um fio de aço, de de comprimento e massa de , é esticado e colocado pra oscilar próximo à extremidade aberta do tubo. O fio, fixo nas duas extremidades, vibra numa frequência correspondente ao segundo harmônico. Essa vibração produz na coluna de ar dentro do tubo uma oscilação que corresponde ao primeiro harmônico. Considere a velocidade do som como
1. Encontre a frequência de oscilação da coluna de ar.
2. Desenha o tubo e faça uma representação transversal(tipo corda) dos nós e antinós de pressão para essa frequência.
3. Calcule a tensão no fio
4. Você está parado a uma distância de uma fonte pontual que emite ondas sonoras de forma isotrópica(igualmente em todas as direções). Ao caminhar em direção à fonte, observa que a intensidade foi dobrada.
2. Calcule a distância