A função de onda para uma onda progressiva em uma corda esticada é ( em unidades do SI):

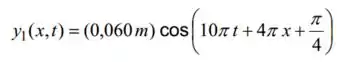
Suponha que a corda possui uma massa por unidade de comprimento de

1. Obtenha o comprimento de onda, a velocidade e o sentido de propagação da onda.
2. Obtenha o valor máximo de velocidade transversal da corda. Para a posição , em que instantes esse valor máximo ocorre?( Dê os dois primeiros, para
3. Determine a tensão na corda e a potência média transmitida por esta onda.
4. Escreva a função de onda que sobreposta a uma função produza uma onda estacionária. Obtenha a função de onda estacionária.
5. Determine as duas primeiras posições para os dois primeiros nós da onda estacionária gerada.

b):

Lembra como a gente calcula a velocidade transversal? É a derivada parcial daquela função lá de cima em relação ao tempo:

Para

Quando a velocidade terá um máximo? Se o que queremos é o maior valor positivo, vai ser quando o “ângulo” do seno for igual a :

E esse é o tempo para o qual temos a velocidade máxima. E velocidade máxima é o valor da função quando o seno for igual a menos 1:

c):

A tensão é facilmente achada, só a gente usar:

Onde é a densidade linear que foi dada no enunciado.

Então:

E a potência média é dada pela formula:

Já temos quase tudo que precisamos pra calcular, só precisamos calcular a

Então:

d):

Isso é muito fácil. Lembra que numa corda onde surge uma onda estacionária existem duas ondas parecidas mas que se deslocam em sentidos contrários?

E lembra que o que marca o sentido de uma onda na equação de onda é o sinal que vem na frente da frequência angular?

Então, se

A outra onda vai ter o sentido contrário:

E ai, basta a gente preencher a equação de uma onda estacionária:

e):

Vão ser as posições que a fazem a equação ser igual a zero. Isso é, quando :

Isso acontece quando:

E:

Resolvendo essas equações: