Interferência
- Na figura abaixo, dois alto-falantes e estão separados por uma distância em um palco ao ar livre. Durante o teste do som, os dois alto-falantes emitem, em fase, sons com comprimento de onda
- Um ouvinte encontra-se inicialmente sobre o eixo a do alto falante e pode se deslocar sobre esse eixo em direção a Considere apenas os valores de .
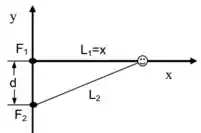
- Encontre as duas posições do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva).
- Em que posição(ões) do ouvinte a intensidade sonora passa por uma máximo(interferência construtiva)?
Passo 1
a):
Aqui a gente vai usar a equação abaixo:
Pela nossa teoria, se quisermos que exista uma interferência destrutiva, a fase vai ter que ser um múltiplo ímpar de Então:
Beleza. Vamos agora montar a expressão pra esse . Perceba que temos ali um triângulo retângulo onde é a hipotenusa, um cateto e o outro. Então:
Então:
Usando
E pra achar a outra posição, vamos fazer a mesma coisa só que para :
Então:
Passo 2
b):
Vamos fazer a mesma coisa que na a), só que agora temos múltiplos pares de . Então:
Vamos usar Então:
Então:
Claro, temos que testar outros valores de . Lembrando que Então:
O que é impossível.
E
Só que não vale né? Queremos
Então a única opção é
Resposta
a):
b):
Exercícios de Livros Relacionados
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr