P2 de Física 2- FIS1041 da PUCRIO - 2014.2

Uma onda senoidal se propaga ao longo de uma corda sob tensão. A figura 1 fornece a inclinação da corda ao longo do eixo no instante . Suponha que a equação da onda progressiva é do tipo

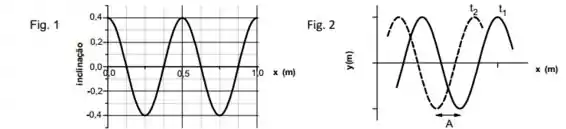
1. Calcule a amplitude da onda progressiva.
2. Calcule a constante de fase.

A figura dois mostra dois instantes diferentes de um pedaço da mesma onda progressiva da figura 1. Na figura , e

3. Calcule a frequência da onda progressiva.
4. Escreva a equação , com os valores pra , e , e com o sinal correto em frente a , baseando-se na análise das figuras 1 e 2.

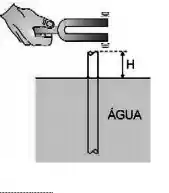
(B)Um tubo de vidro, aberto em ambas as extremidades, de diâmetro e comprimento , é colocado verticalmente na água de um tanque de modo que um pedaço do tubo fique fora da água e acima da linha da água. Faz se vibrar um diapasão na extremidade superior do tubo. Afunda-se o tubo, diminuindo-se lentamente , e verifica-se que os dois maiores valores de para os quais o som tem ampliação são e .

a) Escreva a relação entre e o comprimento de onda da onda sonora para que haja ressonância no tubo.

b) A que modos de vibração correspondem as duas ressonâncias em e ? Calcule a frequência do diapasão.

c) Calcule o(s) outro(s) valor(es) de em que haverá ampliação do som.

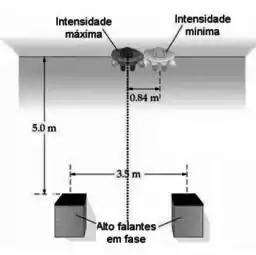
1. Dois alto-falantes estão emitindo em fase e estão afastados por uma distância de à frente (ver figura). Um ouvinte encostado na parede ouve um som de máxima intensidade quando se encontra à mesma distância dos alto-falantes. Ao se deslocar ao longo da parede, a intensidade sonora diminui e passa por um mínimo em

1. Calcule a frequência do som emitido pelos alto-falantes.
2. Suponha que o ouvinte está nessa posição deslocada. Calcule as duas menores frequências que os alto-falantes devem emitir para que seja detectado um máximo de intensidade.

Uma onda estacionária é produzida sobre uma corda pela superposição de duas ondas transversais progressivas dadas por:

Onde e são dados em metros e em segundos.

1. Considere que a corda está submetida a uma tensão de . Encontre a massa por unidade de comprimento da corda.
2. Encontre a expressão da onda resultante ( como produto de duas funções, uma apenas de e outra apenas de
3. Encontre o menor valor positivo de que corresponde a um nó.
4. Considerando o intervalo , encontre os instantes em que a velocidade transversal dos elementos da corda são nulos.
5. Desenhe a corda nos instantes do item d), no intervalo , indicando, claramente as distâncias relevantes.