Interferência
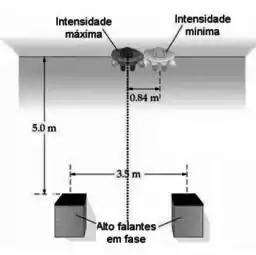
- Dois alto-falantes estão emitindo em fase e estão afastados por uma distância de à frente (ver figura). Um ouvinte encostado na parede ouve um som de máxima intensidade quando se encontra à mesma distância dos alto-falantes. Ao se deslocar ao longo da parede, a intensidade sonora diminui e passa por um mínimo em
- Calcule a frequência do som emitido pelos alto-falantes.
- Suponha que o ouvinte está nessa posição deslocada. Calcule as duas menores frequências que os alto-falantes devem emitir para que seja detectado um máximo de intensidade.
Passo 1
a):
Vamos usar a fórmula:
Vamos calcular usando o fato de que quando ele se desloca m pra direita, ele passa a ouvir um mínimo.
Para que haja um mínimo, tem que ser um múltiplo ímpar de
Além disso:
E
Usamos pitagoras ali (:
Passo 2
Então:
Beleza!
Como a fase tem que ser um múltiplo ímpar de , vamos toma-la como igual ao próprio
Com o valor de :
Passo 3
b):
Agora a situação é um pouco diferente. Temos ainda a mesma diferença de caminhos , só que agora precisamos adaptar a frequência pra que ela gere um mínimo.
Os mínimos ocorrem quando a diferença de fase é um múltiplo par de
Vamos usar então e
E:
Resposta
a):
b):
Exercícios de Livros Relacionados
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr