Uma onda estacionária é produzida sobre uma corda pela superposição de duas ondas transversais progressivas dadas por:
Onde e são dados em metros e em segundos.
- Considere que a corda está submetida a uma tensão de . Encontre a massa por unidade de comprimento da corda.
- Encontre a expressão da onda resultante ( como produto de duas funções, uma apenas de e outra apenas de
- Encontre o menor valor positivo de que corresponde a um nó.
- Considerando o intervalo , encontre os instantes em que a velocidade transversal dos elementos da corda são nulos.
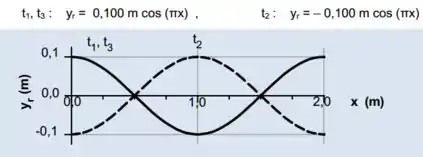
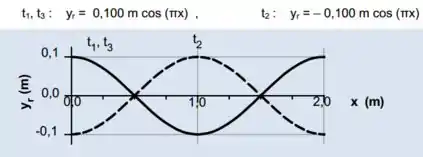
- Desenhe a corda nos instantes do item d), no intervalo , indicando, claramente as distâncias relevantes.
Passo 1
a):em galera, quando se fala de tensão e densidade linear( massa por unidade de comprimento), a gente lembra disso:
Então:
Bem, já temos a tensão. Basta achar a velocidade.
A velocidade a gente encontra analisando a fórmula:
Lembrando que essa equação segue o padrão:
A gente percebe que:
Maaas, agora, a gente tem que lembrar da relação:
Pronto! Achamos a velocidade. Então jogamos na fórmula:
Passo 2
b):
Sabemos que a soma de duas ondas que são idênticas mais se propagam em direções opostas, gera uma onda estacionária. Essa onda é:
Você pode perceber isso fazendo aquela soma de cossenos, mas é interessante lembrar desse resultando, pra não ter que ficar usando trigonometria na hora da prova.
Assim:
Com em metros e em segundos.
Passo 3
c):Pra que tenha um nó, precisamos ter . Afinal de contas, o nó sempre fica parado e nunca oscila , certo?
Então, pra que haja um nó, devemos ter:
O menor valor pra ocorre quando
Passo 4
d):
Lembra da velocidade transversal? Ela é dada pela derivada parcial da função em relação ao tempo. Então:
Bom, igualzinho ao c), só é igual à zero quando:
E isso acontece quando:
E
Para os valores de :
Passo 5
e):
Resposta
a):
b):
c):
d):
e):