(B)Um tubo de vidro, aberto em ambas as extremidades, de diâmetro e comprimento , é colocado verticalmente na água de um tanque de modo que um pedaço do tubo fique fora da água e acima da linha da água. Faz se vibrar um diapasão na extremidade superior do tubo. Afunda-se o tubo, diminuindo-se lentamente , e verifica-se que os dois maiores valores de para os quais o som tem ampliação são e .
a) Escreva a relação entre e o comprimento de onda da onda sonora para que haja ressonância no tubo.
b) A que modos de vibração correspondem as duas ressonâncias em e ? Calcule a frequência do diapasão.
c) Calcule o(s) outro(s) valor(es) de em que haverá ampliação do som.
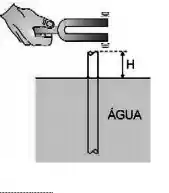
Passo 1
a):
Como uma parte do tubo vai estar colado na água e a outra vai estar aberta pro ar, podemos considerar que a parte que ficará pra fora da água formará um tubo sonoro fechado em uma extremidade, esse tendo comprimento .
Então, pra se ter ressonância:
Passo 2
b):
Nós temos, pra dois valores diferentes de , e
E:
Dividindo uma equação pela outra:
Agora, como e são impares, podemos dizer que:
Então:
Resolvendo:
Usando:
Então:
Passo 3
c):
Usando aquela fórmula:
Para
Resposta
a):
b):
c):