P2 de Física 2- FIS1041 da PUCRIO - 2018.1

Em uma corda é observada uma onda cuja função de onda é dada por:

onde e estão em centímetros e t em segundos. Determine:

1. O comprimento de onda e a frequência das duas ondas progressivas que formam a onda acima;
2. A velocidade de propagação das ondas na corda;
3. As funções de onda, ) e das duas ondas que geram a onda acima;
4. A posição dos nós na corda;
5. Mostre que a onda obedece à equação de onda.
6. Sabendo que a corda está vibrando no quarto harmônico, com extremidades fixas, represente graficamente a onda e determine o comprimento da corda.

Uma fonte pontual emite 25,0 W de som isotropicamente. Um pequeno microfone intercepta o som em uma área de , a da fonte. Calcule:

1. A intensidade sonora e o nível sonoro na posição do microfone.
2. A amplitude de variação de pressão correspondente a essa intensidade.
3. A potência interceptada pelo microfone.

Duas frequências de ressonância sucessivas de um tubo de órgão são , .

4. O tubo está fechado em uma extremidade e aberto na outra ou está aberto nas duas extremidades? Justifique.
5. Determine o comprimento do tubo.

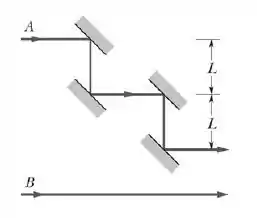
Considere duas ondas sonoras, e , de mesma amplitude, , que se propagam da esquerda para a direita seguindo dois diferentes percursos (ver figura). As duas ondas têm o mesmo comprimento de onda, , e estão inicialmente em fase. A onda é refletida por 4 superfícies espaçadas por distâncias , como indica a figura, mas volta a se propagar na direção e no sentido original. No final, e se superpõem produzindo um fenômeno de interferência. Obtenha, em função de , os dois maiores valores de para que a interferência entre e seja:

1. completamente destrutiva;
2. completamente construtiva;
3. Obtenha a diferença de fase, , entre e no final dos percursos, em função de e .
4. Escreva a amplitude da onda resultante, , em função da amplitude de cada onda e da diferença de fase .
5. Calcule, em função de , o maior valor de para que a amplitude resultante seja igual à amplitude de cada onda, separadamente.