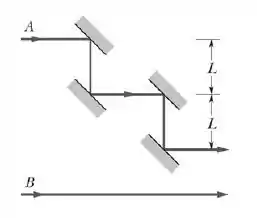
Considere duas ondas sonoras, e , de mesma amplitude, , que se propagam da esquerda para a direita seguindo dois diferentes percursos (ver figura). As duas ondas têm o mesmo comprimento de onda, , e estão inicialmente em fase. A onda é refletida por 4 superfícies espaçadas por distâncias , como indica a figura, mas volta a se propagar na direção e no sentido original. No final, e se superpõem produzindo um fenômeno de interferência. Obtenha, em função de , os dois maiores valores de para que a interferência entre e seja:
- completamente destrutiva;
- completamente construtiva;
- Obtenha a diferença de fase, , entre e no final dos percursos, em função de e .
- Escreva a amplitude da onda resultante, , em função da amplitude de cada onda e da diferença de fase .
- Calcule, em função de , o maior valor de para que a amplitude resultante seja igual à amplitude de cada onda, separadamente.
Passo 1
a) Na interferência destrutiva, temos que a diferença de fase é
, ou
No nosso exercício é possível observar na figura que , portanto:
, com
Rearranjando a equação acima, temos:
Ao substituir valores para , vemos que os dois maiores valores de se dá quando e , com e , respectivamente.
Passo 2
b) Quando a interferência é construtiva:
ou
Seguindo o mesmo procedimento anterior e calculando para , obtemos , e quando , .
Passo 3
c) Bom pessoal, lembra de quando estudamos diferença de fase entre duas ondas?!
Pois bem, lá na nossa teoria diz que a diferença de fase entre A e B se dá por:
E como , obtemos:
Passo 4
d) Bom, amplitude da onda é descrita da forma:
Onde,
Portanto, substituindo e somando as equações:
Passo 5
e) O maior valor de se dá quando a amplitude da onda resultante () for igual a amplitude da onde .
Para isso utilizando da última equação descrita no passo 4, temos:
Resposta
A) e
B) e
C)
D)
E)