Em uma corda é observada uma onda cuja função de onda é dada por:
onde e estão em centímetros e t em segundos. Determine:
- O comprimento de onda e a frequência das duas ondas progressivas que formam a onda acima;
- A velocidade de propagação das ondas na corda;
- As funções de onda, ) e das duas ondas que geram a onda acima;
- A posição dos nós na corda;
- Mostre que a onda obedece à equação de onda.
- Sabendo que a corda está vibrando no quarto harmônico, com extremidades fixas, represente graficamente a onda e determine o comprimento da corda.
Passo 1
A) Bom, nós sabemos lá da introdução a ondas que a equação da onda harmônica é algo do tipo:
,
Observando a equação podemos extrair dados como e da nossa equação. Onda e .
E o comprimento e a frequência de uma onda é dado por, e respectivamente.
Então basta substituirmos os valores dados no enunciado na fórmula para que obtenhamos e .
Passo 2
B) A velocidade de propagação de uma onda, se da por:
Passo 3
C) Para resolver esse tópico, temos de lembrar das propriedades do seno. Quando somamos:
Portanto, podemos descrever as duas equações como:
Passo 4
D) Para acharmos os nós na corda, é necessário verificar a amplitude é zero, ou seja, a nossa equação tem de ser igual a zero.
Pela equação:
obtemos:
Passo 5
E) A equação da onda da onda é dada por:
Portanto precisamos achar as derivamos e substitui-las posteriormente para comprovar que a onda obedece a equação. As derivadas são:
Substituindo as derivadas acima na equação da onda, temos:
Passo 6
F)
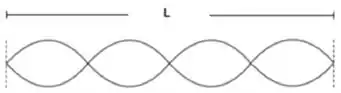
Como , obtemos que
Resposta
A) e
B)
C) ;
D)
E)
F)