2º EE de Física 3 da UFPE - 2016.1

No circuito mostrado na figura abaixo, a chave é fechada no instante . A carga no capacitor neste instante é .

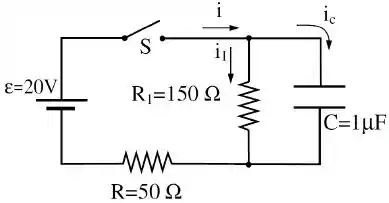
Para tal situação, calcule:

As correntes e no instante .

As correntes e para .

A energia potencial elétrica acumulada no capacitor, quando o mesmo está totalmente carregado.

A constante de tempo do circuito.

Um capacitor cilíndrico é constituído por duas cascas cilíndricas metálicas e coaxiais. A casca interna possui raio e carga , enquanto que a casca externa possui raio e carga . Ambas as cascas possuem comprimento .

Calcule a capacitância do capacitor.

Calcule a densidade de energia eletrostática armazenada no interior do capacitor.

Utilize o campo elétrico obtido no item , e calcule a energia armazenada no interior do capacitor.

Um dielétrico de constante dielétrica é colocado entre as placas do capacitor de maneira a preencher todo espaço entre elas. Nestas circunstâncias, calcule o campo elétrico no interior do capacitor e as cargas induzidas na superfície do dielétrico, .

Na figura abaixo, duas partículas pontuais, de massas distintas e , e cargas elétricas idênticas e positivas de valor , deslocam-se ao longo do eixo com velocidades constantes dadas por .

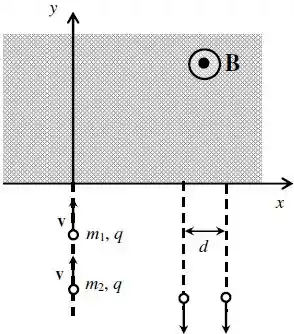
Tais partículas penetram a região , onde existe um campo magnético uniforme , perpendicular ao plano e saindo do plano da página.

Considere que o campo magnético é nulo fora da região . Sabe-se que, ao saírem da região , as partículas movem-se em trajetórias retilíneas e paralelas entre si.

Calcule o comprimento das trajetórias descritas pelas partículas, na região .

Calcule o trabalho realizado pela força magnética sobre as partículas, durante o deslocamento das mesmas na região .

Neste item, assuma que , e que é conhecida, enquanto que é desconhecida. Sabe-se também que as partículas, ao saírem da região , cruzam o eixo separadas por uma distância (veja figura). Nestas circunstâncias, calcule o valor da massa desconhecida , em função das grandezas conhecidas , , , e .