2º EE de Física 3 da UFPE - 2016.2

A figura ao lado ilustra um capacitor de placas esféricas de raios e , com .

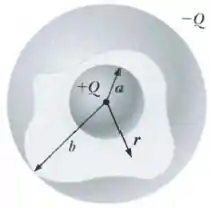
A placa interna tem carga e a placa externa uma carga , com . Há vácuo entre as placas metálicas e a permissividade elétrica do vácuo é denotada por .

Determine o módulo do campo elétrico na região interna do capacitor, , onde é a distância ao centro do capacitor.

Calcule a diferença de potencial entre as placas do capacitor.

Determine a capacitância do capacitor.

Calcule a energia elétrica armazenada no capacitor.

Se a região entre as placas do capacitor for totalmente preenchida com um dielétrico de constante dielétrica , qual é o valor da nova capacitância?

Qual é o valor da diferença de potencial entre as placas do capacitor após a introdução do dielétrico?

No circuito mostrado na figura abaixo, os resistores possuem resistências e as forças eletromotrizes das fontes ideais são e .

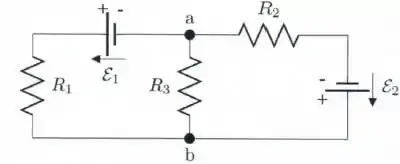
Para tal situação, calcule:

O valor absoluto e o sentido da corrente elétrica que passa através do resistor 1.

O valor absoluto e o sentido da corrente elétrica que passa através do resistor 2.

A diferença de potencial entre os pontos e .

Na figura abaixo, uma carga elétrica pontual (com ), de massa , desloca-se ao longo do eixo com uma velocidade constante de módulo .

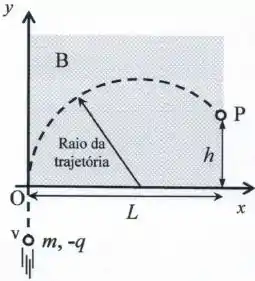
Na origem do sistema de coordenadas (ponto ), tal partícula penetra numa região retangular de largura , onde existe um campo magnético uniforme que é perpendicular ao plano .

Considere que o campo magnético é nulo fora da região hachurada indicada na figura. Depois de percorrer uma trajetória circular (curva tracejada na figura), a partícula abandona a região de campo magnético no ponto , localizado a uma altura em relação ao eixo .

Determine o sentido do campo magnético (entrando ou saindo do plano ). Justifique brevemente sua resposta.

Determine o módulo da velocidade da partícula no ponto . Justifique brevemente sua resposta.

Calcule o raio da trajetória em função de e .

Calcule a altura em função de e .