No circuito mostrado na figura abaixo, a chave é fechada no instante . A carga no capacitor neste instante é .
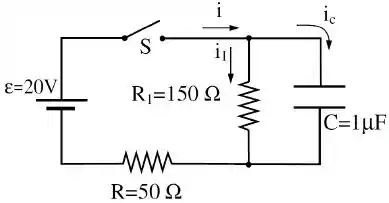
Para tal situação, calcule:
As correntes e no instante .
As correntes e para .
A energia potencial elétrica acumulada no capacitor, quando o mesmo está totalmente carregado.
A constante de tempo do circuito.
Passo 1
As correntes e no instante .
Durante o carregamento, a corrente através do capacitor varia da seguinte forma:
Assim, quando , temos:
Ou seja, nesse instante o capacitor está em curto e toda a corrente passa através dele, logo:
Passo 2
As correntes e para .
Quando a corrente no capacitor tende a zero. Nesse caso, toda a corrente agora passa pelo resistor . Logo:
Utilizando a Lei das Malhas na malha interna, temos:
Passo 3
A energia potencial elétrica acumulada no capacitor, quando o mesmo está totalmente carregado.
A energia potencial elétrica no capacitor é dada por:
Para calcular a carga, vamos utilizar a Lei das Malhas na malha externa:
Substituindo os valores, teremos:
Assim, a energia potencial elétrica acumulada no capacitor carregado será:
Passo 4
A constante de tempo do circuito.
A constante de tempo capacitiva é dada por:
Logo:
Resposta