No circuito mostrado na figura abaixo, os resistores possuem resistências e as forças eletromotrizes das fontes ideais são e .
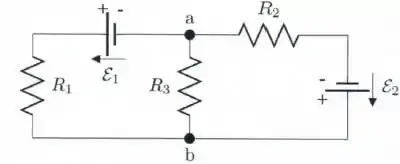
Para tal situação, calcule:
O valor absoluto e o sentido da corrente elétrica que passa através do resistor 1.
O valor absoluto e o sentido da corrente elétrica que passa através do resistor 2.
A diferença de potencial entre os pontos e .
Passo 1
O valor absoluto e o sentido da corrente elétrica que passa através do resistor 1.
Vamos começar a resolver o problema arbitrando os sentidos das correntes , e que passam pelos resistores , e , respectivamente:
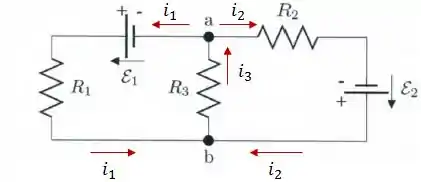
Utilizando a Lei dos Nós no nó , teremos:
Agora vamos aplicar a Lei das Malhas em duas malhas. A malha é formada pelos resistores e , e a fonte , enquanto a malha é formada pelos resistores e , e a fonte .
Percorrendo as duas malhas no sentido anti-horário, teremos, para a malha :
Substituindo os valores, teremos:
Para a malha , teremos:
Substituindo os valores, teremos:
Passo 2
Substituindo as expressões que encontramos na Lei das Malhas na expressão que encontramos na Lei dos Nós, teremos:
Onde :
Onde :
Organizando a bagunça, teremos:
Obs.: Como o valor que encontramos é positivo, a corrente está no sentido que chutamos lá no início, ou seja, no anti-horário.
Passo 3
O valor absoluto e o sentido da corrente elétrica que passa através do resistor 2.
Agora que já descobrimos o valor de , podemos encontrar o valor das outras correntes:
Onde , logo:
Agora podemos encontrar o valor de através da expressão:
Como o valor que encontramos é positivo, o sentido que chutamos no início do problema está certo. Logo, a corrente está no sentido horário.
Passo 4
A diferença de potencial entre os pontos e .
Entre os pontos e temos que:
Substituindo os valores, teremos:
Resposta
; No sentido anti-horário.
; No sentido horário.