Na figura abaixo, uma carga elétrica pontual (com ), de massa , desloca-se ao longo do eixo com uma velocidade constante de módulo .
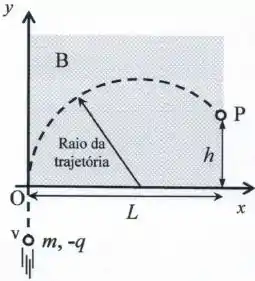
Na origem do sistema de coordenadas (ponto ), tal partícula penetra numa região retangular de largura , onde existe um campo magnético uniforme que é perpendicular ao plano .
Considere que o campo magnético é nulo fora da região hachurada indicada na figura. Depois de percorrer uma trajetória circular (curva tracejada na figura), a partícula abandona a região de campo magnético no ponto , localizado a uma altura em relação ao eixo .
Determine o sentido do campo magnético (entrando ou saindo do plano ). Justifique brevemente sua resposta.
Determine o módulo da velocidade da partícula no ponto . Justifique brevemente sua resposta.
Calcule o raio da trajetória em função de e .
Calcule a altura em função de e .
Passo 1
Determine o sentido do campo magnético (entrando ou saindo do plano ). Justifique brevemente sua resposta.
Em casos de trajetória circular, a força magnética funciona como uma força centrípeta. Nesse caso, ela deve sempre apontar para o centro da trajetória.
A força magnética é dada por:
Dado que a carga elétrica é negativa.
Assim, quando a carga passa pela origem, temos que:
Assim, utilizando a regra da mão direita, concluímos que o campo magnético deve ter o sentido do vetor . Ou seja, entrando no plano .
Passo 2
Determine o módulo da velocidade da partícula no ponto . Justifique brevemente sua resposta.
A força magnética não realiza trabalho, e isso pode ser provado através do raciocínio abaixo:
Onde , logo, substituindo a expressão da força magnética, teremos:
O produto vetorial nos dará um vetor perpendicular a , e como o produto escalar entre vetores perpendiculares é nulo:
Beleza. No entanto, o trabalho realizado sobre um corpo é igual à variação da energia cinética.
Assim, como o trabalho resultante é nulo, variação de energia cinética é nula. Logo, a variação de velocidade será nula.
Finalmente:
Passo 3
Calcule o raio da trajetória em função de e .
Como eu disse no Passo 1, a força magnética nesse caso funciona como força centrípeta, logo:
Onde é o raio da trajetória circular.
Arrumando os termos, teremos:
Passo 4
Calcule a altura em função de e .
A partir da figura, podemos formar um triângulo retângulo de hipotenusa igual a . Se liga:
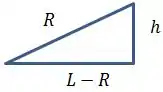
Assim, usando Pitágoras, teremos:
Substituindo a expressão de que encontramos no Passo 3, teremos:
Resposta
O campo magnético tem sentido entrando no plano .