A figura ao lado ilustra um capacitor de placas esféricas de raios e , com .
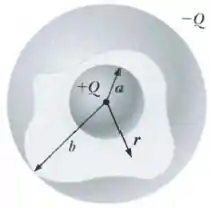
A placa interna tem carga e a placa externa uma carga , com . Há vácuo entre as placas metálicas e a permissividade elétrica do vácuo é denotada por .
Determine o módulo do campo elétrico na região interna do capacitor, , onde é a distância ao centro do capacitor.
Calcule a diferença de potencial entre as placas do capacitor.
Determine a capacitância do capacitor.
Calcule a energia elétrica armazenada no capacitor.
Se a região entre as placas do capacitor for totalmente preenchida com um dielétrico de constante dielétrica , qual é o valor da nova capacitância?
Qual é o valor da diferença de potencial entre as placas do capacitor após a introdução do dielétrico?
Passo 1
Determine o módulo do campo elétrico na região interna do capacitor, , onde é a distância ao centro do capacitor.
Pra calcular o campo elétrico, vamos utilizar a Lei de Gauss, aproveitando a simetria esférica do problema. Logo:
Nesse caso, a nossa gaussiana é uma esfera de raio , onde , e que envolve a placa interna com carga .
Portanto:
Passo 2
Calcule a diferença de potencial entre as placas do capacitor.
O potencial elétrico está relacionado com o campo elétrico através da seguinte equação:
Substituindo a expressão de que encontramos no primeiro item e fazendo a integral entre e , teremos:
Finalmente:
Passo 3
Determine a capacitância do capacitor.
A capacitância está associada à diferença de potencial por:
Substituindo a expressão da diferença de potencial, teremos:
Finalmente:
Passo 4
Calcule a energia elétrica armazenada no capacitor.
A energia elétrica em um capacitor é dada por:
Substituindo a expressão da capacitância, teremos:
Organizando esse cara, teremos:
Passo 5
Se a região entre as placas do capacitor for totalmente preenchida com um dielétrico de constante dielétrica , qual é o valor da nova capacitância?
Se a região for preenchida por um material dielétrico, a permissividade elétrica vai deixar de ser para ser , onde:
Logo, substituindo isso na expressão da capacitância, teremos:
Passo 6
Qual é o valor da diferença de potencial entre as placas do capacitor após a introdução do dielétrico?
Novamente, quando colocamos o dielétrico, a permissividade deixa de ser para ser . Assim, substituindo isso na expressão do potencial elétrico, teremos:
Resposta