Dados os conjuntos
Escreva na notação de intervalo e represente graficamente o conjunto
Passo 1
Você que me acompanha aqui, sabe que agora eu diria pra começar do começo. Mas qual é o fuc***ng começo? Hahaha vamos começar dos parênteses ok?
Precisamos de , saca só o desenho:
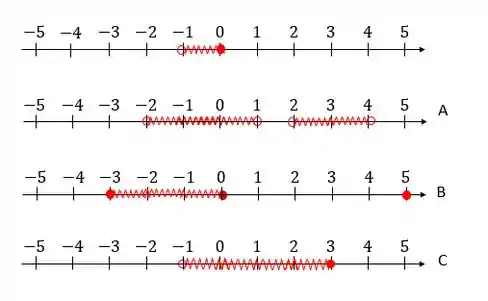
Essa primeira linha tem exatamente aquilo que procuramos: a interseção entre os três conjuntos, ou seja, aqueles números que estão presentes nos três conjuntos. Na notação de intervalo:
Passo 2
Agora vamos atrás do :
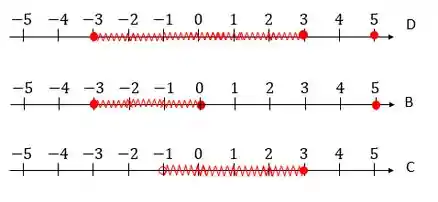
Veja que
Escrevendo na notação de intervalo:
Mas o que a questão quer é justamente o complementar disto, ou seja, tudo aquilo na reta que não seja o . Se liga como fica no desenho:
![]()
Percceba que as bolinhas fechadas viram bolinhas abertas e preenchemos tudo aquilo que estava preenchido. Escrevendo isso na notação de intervalo:
Passo 3
Maneiro, esse cara ta estranho, mas vida que segue! Vamos agora realizar a operação:
Escrevendo na notação de intervalo:
Perceba que são intervalos/conjuntos disjuntos, então não temos como simplificar esse termo. Pensa neles como quatro tracinhos numa reta que não se tocam.
Passo 4
Vamos enfim para o último passo, que é realizar a última operação:
Então, na representação gráfica, ficamos com:
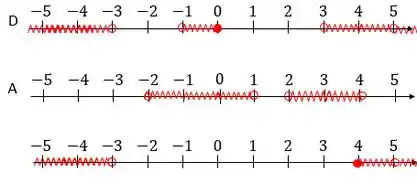
A última linha nos dá o resultado dessa contarada toda. Vamos escrever isso na notação de intervalo: