No SIMULINK, gere o gráfico da função:
E o gráfico de multiplicado por .
Passo 1
O exercício pede para plotarmos os gráficos de e de . Para isto, construiremos um modelo com sete blocos:
- A entrada do modelo é composta por três blocos. Dois deles servirão para obter : um bloco “Constant”, que deverá ser igual a , e um bloco “Sine Wave”, representando o componente de . O terceiro bloco é um bloco “Constant”, que será igual a e servirá para gerar ;
- Um bloco para somar os dois blocos de entrada que produzem , chamado “Add”;
- Um bloco para fazer o produto entre e o bloco “Constant” igual a , para gerar ;
- A saída do modelo será dois blocos “Scope”, que plotarão e .
Passo 2
Vamos começar com as duas entradas para construir , primeiramente com o bloco “Constant”. Vá à biblioteca “Sources”, ache o bloco “Constant” e arraste-o para um modelo em branco:
Para atribuir o valor de a ele, clique duas vezes sobre o bloco que você acabou de inserir, para acessar os seus parâmetros:

No campo do parâmetro “Constant value”, destacado acima, altere o valor padrão de para .
Agora, adicione a segunda entrada para construir : o bloco “Sine Wave”. Ainda na biblioteca “Sources”, encontre o bloco “Sine Wave” e arraste-o para o modelo.
Clique duas vezes sobre o bloco que você acabou de inserir para ver seus parâmetros:

Segundo a própria janela com os parâmetros do bloco, uma onda senoidal gerada por ele tem essa sintaxe:
A onda que queremos criar é , logo a amplitude é , a frequência é , a fase é e o é . Esses são os parâmetros destacados em vermelho acima. Note que não precisamos alterar nada nas propriedades. Simplesmente feche a janela de propriedades e vá para o passo 3.
Passo 3
Após adicionar as duas entradas que geram , vamos inserir o bloco “Add” para somá-las. Selecione a biblioteca “Math Operations”, procure o bloco “Add” e arraste-o para o nosso modelinho:

Conecte os blocos “Constant” e “Sine Wave” a cada uma das entradas de “Add” e o modelo ficará com essa cara:
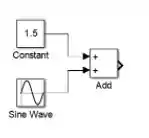
A saída de “Add” será , pois .
Passo 4
Vamos inserir a terceira e última entrada do modelo: um bloco “Constant” com valor de , que servirá para calcular . Vá à biblioteca “Sources” novamente para buscar o bloco. Arraste-o para o modelo e altere seu valor para , seguindo as instruções apresentadas no passo 2 da resolução deste exercício. O modelo ficará assim:
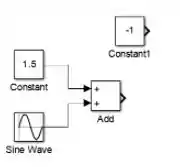
Com o modelo atual, já podemos inserir o bloco que fará a operação cujo resultado será : o bloco “Product”. Encontre-o na biblioteca “Math Operations” e arraste-o para o modelo:
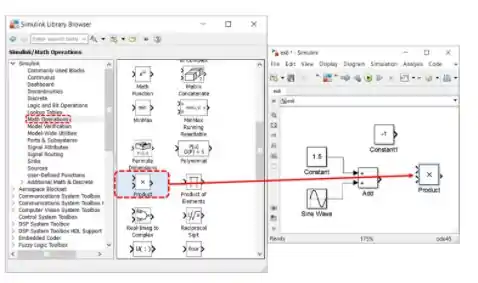
O bloco “Product” multiplicará por , resultando em . Para fazer essa operação, devemos conectar o bloco “Constant” com valor e a saída de “Add” (que á função ) a cada uma das entradas de “Product”:
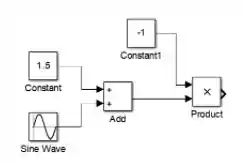
A saída de “Product” será .
Passo 5
Hora de inserir as saídas do modelo! Como queremos dois gráficos, um para e outro para , vamos adicionar dois blocos “Scope”. Para isto, vá à biblioteca “Sinks” e arraste dois blocos “Scope” para o modelo:

Conecte a saída de “Product” a um “Scope”, o qual vai plotar :
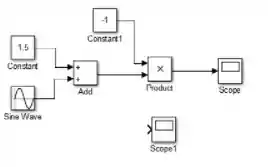
Conecte o segundo “Scope” à saída de “Add”, para plotar . Para isto, clique sobre a seta na lateral do “Scope” e arraste, aparecerá uma flecha vermelha tracejada:
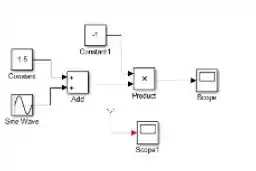
Conecte a outra ponta da flecha na linha conectando “Add” a “Product”, o modelo ficará assim:
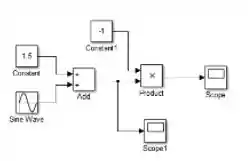
Reparou que apareceu uma bolinha preta onde você acabou de conectar? Essa conexão faz com que a saída de “Add” (lembrando que essa saída é ) vá para o bloco “Product” E para o bloco “Scope”. Dessa forma, consegue-se calcular e também plotar .
Passo 6
Nosso modelinho está pronto! Para gerar os gráficos, rode o programa e, ao final da execução, clique duas vezes sobre cada um dos blocos “Scope” para visualizar as curvas de e .
Resposta
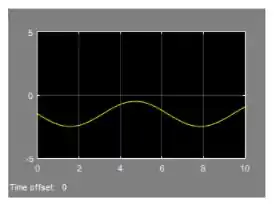
O gráfico de é:
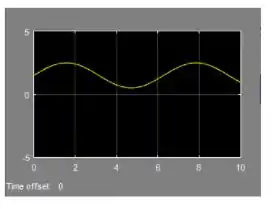
O gráfico de é: