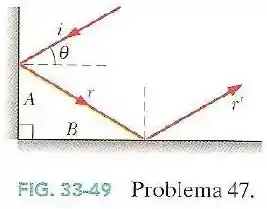
A Fig.33-49 mostra um raio luminoso sendo refletido em dois espelhos perpendiculares e .
Determine o ângulo entre o raio incidente e o raio .
Passo 1
Quando um raio luminoso é refletido, o ângulo que o raio refletido faz com a direção normal à superfície é igual ao ângulo que o raio incidente faz.
No nosso caso, temos que o ângulo de com a normal ao espelho vai ser .
Passo 2
Sabendo o ângulo entre e a direção perpendicular ao espelho , podemos encontrar o ângulo que faz com a normal ao espelho .
O raio vai fazer um ângulo com o espelho , fazendo em troca um ângulo com o espelho e um ângulo de com a normal ao espelho .
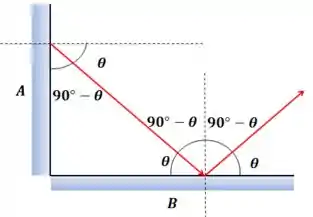
Como o ângulo de reflexão é igual ao ângulo de incidência, também fará um ângulo com a normal ao espelho e um ângulo com o próprio espelho.
Passo 3
O espelho é perpendicular ao espelho e por isso sua normal é paralela ao espelho .
Isso significa que se faz um ângulo com a normal à , ele também o faz com o espelho e, logo, ele é paralelo ao raio refletido porém com sentidos opostos.
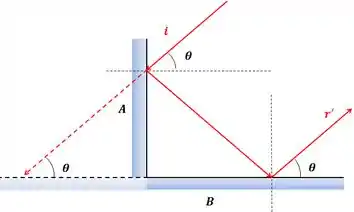
Com isso vemos que o ângulo entre e é de .
Resposta
O ângulo entre e é de .