Uma amperiana de raio igual a envolveu 4 cabos de transmitiam correntes diferentes, como pode ser visto na figura abaixo:
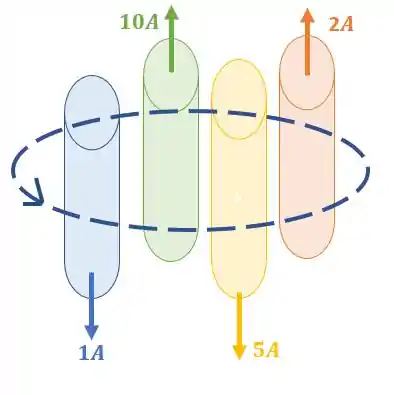
Considerando a orientação da curva amperiana, determine o módulo do campo magnético.
Dado:
Considere: .
Passo 1
Vamos começar pensando na Lei de Ampère que nos diz:
Integrando o campo em todo a curva , encontramos:
Onde é o comprimento da curva, é o ângulo entre o campo magnético e a curva e é toda a corrente interna a curva.
Passo 2
Agora que já sabemos sobre a fórmula, vamos começar a descobrir quanto vale cada coisa.
O primeiro é que como as correntes mais elevadas apontam para cima, pela regra da mão direita o campo que envolve esses fios está na mesma direção da curva amperiana que circula os cabos:
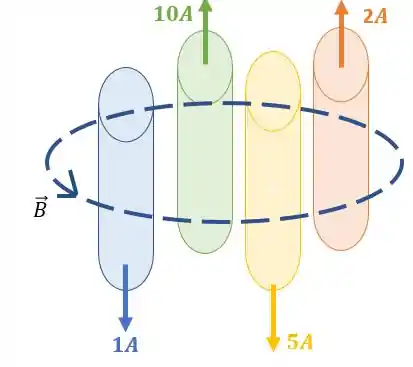
Ou seja, isso quer dizer que o ângulo entre a curva e o campo magnético é zero:
Logo o cosseno do ângulo é igual a:
Ótimo achamos já uma informação!
Passo 3
Vamos pensar no comprimento da curva, como o desenho é uma curva em círculo, podemos achar o tamanho da curva a partir do comprimento do círculo que segue a fórmula:
Sabemos que nossa curva tem raio igual a:
Logo, substituindo na fórmula e considerando :
Passo 4
Agora a única informação que nos falta reunir é a corrente interna a curva amperiana.
Como consideramos lá no início que a corrente estava direcionada para cima, todas as componentes que tiverem para baixo serão subtraídas da nossa conta, certo?
Por exemplo, as correntes que estão para cima são a verde e a rosa, então elas são positivas:
Enquanto as correntes que estão para baixo são a azul e a amarela, então elas são negativas:
Dessa forma, a corrente interna total é igual a:
Passo 5
Agora que tal substituirmos tudo que levantamos de dados na fórmula:
Substituindo:
E o que foi dado no enunciado:
Teremos:
Queremos saber o módulo do campo magnético , então precisamos isolar ele de um lado só da igualdade:
Podemos substituir o valor de , logo:
A multiplicação dos números no numerador é igual a:
Então:
Vamos dividir por :
Pronto, encontramos o módulo do campo magnético gerado por todos os fios juntos!