Dado que a Lei de Ampère define que o campo magnético dado no interior de um solenóide de comprimento , número de espiras igual a e corrente :
Qual deve ser o número de espiras para que o campo magnético seja igual a , quando o e a corrente é igual a ?
Dado:
Considere: .
Passo 1
Bom pessoal, o enunciado nos explica que podemos calcular o campo magnético no interior de um solenóide, através de uma superfície amperiana!
Logo, o módulo do campo magnético informado pelo enunciado para um solenóide é igual a:
Percebe que o campo não depende de uma característica específica da amperiana, depende das característas do solenóide, uma vez que a amperiana acompanha a parte interna do solenoide:
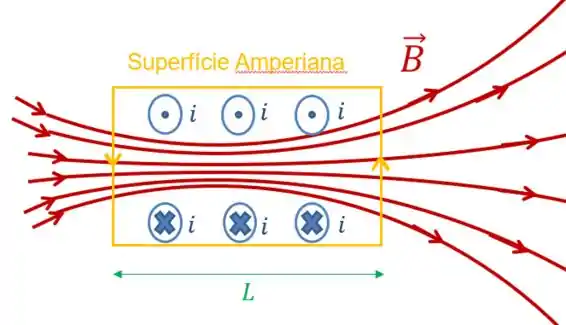
Ou seja, depende da corrente , do número de espiras (que queremos descobrir), do comprimento do solenóide e da permeabilidade magnética do vácuo !
Passo 2
Vamos fazer um levantamento dos dados fornecidos no enunciado:
Veja que o raio não está em metros, e sim, em centímetros, para continuar com os cálculos, precisamos passar para metros. Para isso, basta dividir por :
Passo 3
Substituindo esses valores na fórmula do campo magnético:
Teremos então:
Como desejamos calcular , vamos isolar essa incógnita do problema passando todos os números para o outro lado da igualdade!
O que estava dividindo , passa para o outro lado multiplicando:
A parcela que multiplicava , irá para o outro lado dividindo:
Considerando como foi dito no enunciado:
Realizando as multiplicações no numerador e no denominador:
Como temos uma divisão por uma potência de , podemos passar essa potência para o numerador desde que invertamos o sinal do expoente:
Assim, multiplicando por :
Dividindo por :
Ou seja, necessitamos de um solenóide com vinte e cinco mil espiras!