Vigas – Efeitos externos
Produzido por Pablo RicardoTeoria
Introdução
Nesse tópico vamos abordar as vigas. Mas o que é uma viga?

Viga é esse elemento estrutural horizontal e ela participa da transmissão de cargas que chegam no solo. Existem diversos elementos de máquinas que têm comportamento equivalente ao de uma viga, por isso seu estudo é tão importante em diversas áreas.
O que vamos estudar aqui é o seguinte: O que acontecerá se uma força for aplicada em uma viga, como mostrado abaixo?
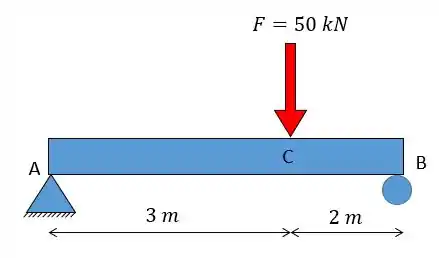
Para começar a entender esse tipo de problema a gente tem que entender os apoios (que estão representados em e ).
Apoios e Reações
Antes de tudo vamos relembrar uma coisa muito importante: Reações de apoio só surgem onde há impedimento de movimento. Então, se algum apoio não permitir que uma estrutura se mova no eixo , por exemplo, você coloca uma reação . Vamos ver os principais apoios:
- Apoios que impedem um movimento, chamados apoios de 1° gênero:
- Apoios que impedem dois movimentos, chamados de apoios de 2° gênero. São os pinos, por exemplo:
- Apoios que impedem dois movimentos e a rotação, chamados de apoios de 3° gênero: esses são os engastes, quando parte de uma viga está embutida dentro de uma parede, por exemplo. A diferença é que aqui temos também um momento como reação.

Repare que esse apoio é um rolete, ou seja, ele permite que a viga se mova na horizontal, mas não permite que ela se desloque na vertical. Então, o que fazemos neste caso? Substituímos o apoio por uma reação na direção em que não há movimento, assim:
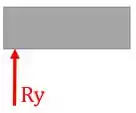
Esse mesmo apoio pode ser representado por essas formas aqui:
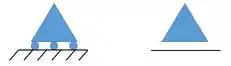
Já sabe, se aparecer algum desses apoios eles impedem movimento em uma direção!!!![]()

Outra forma de representar esse tipo apoio é:
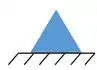
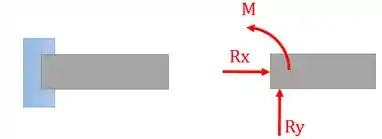
Esse apoio pode aparecer para você assim:

Voltando ao nosso exemplinho a gente tinha isso aqui:
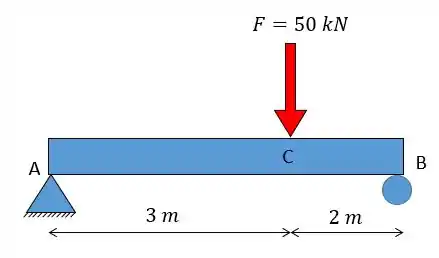
Logo, temos um apoio de 2° gênero em e um rolete (apoio de primeiro gênero) em . Portanto, as reações vão ficar da seguinte forma:
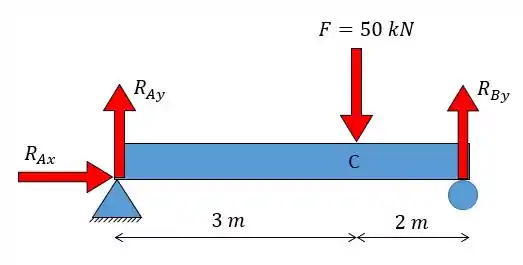
Tipos de Viga
Viga em balanço: são aquelas que possuem uma parte “balançando”, sem apoios. Normalmente essas vigas vão estar presas por engastes, mas podem estar apoiadas em pinos e roletos também.


Viga com apoios simples: essas vão ter suas extremidades sempre presas (apoiadas ou engastadas).
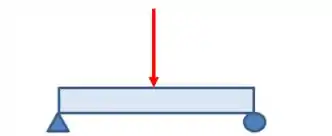
Lembre-se que a reação depende do tipo de apoio, independentemente da viga estar em balanço ou não. Mas é muito importante saber o que é uma viga em balanço porque com certeza você verá isso!
Efeitos Externos
Os efeitos externos da aplicação de uma força numa viga são justamente as reações. E como fazemos para calcular? Vamos voltar ao nosso problema, já com as reações:
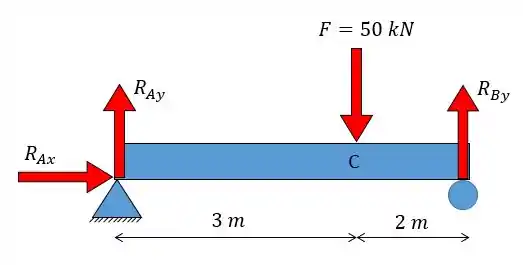
Basicamente, uma viga deve atender as condições de equilíbrio da mecânica, ou seja:
Então para a nossa viga vamos ter três equações:
Aí agora é calcular cada uma dessas três equações, lembrando de sempre considerar as direções positivas e negativas, vamos começar pelo somatório das forças em e considerar tudo que é para a direita positivo:
Perceba que existe apenas uma força em , que é a reação horizontal no apoio. Como essa viga está estática, então essa força deve ser zero!
Vamos agora para a força em , considerando as forças positivas para cima:
Ainda não podemos resolver então vamos para o momento, considerando o momento positivo no sentido horário e aplicado ao ponto (você pode aplicar em ou , tanto faz belezinha?):
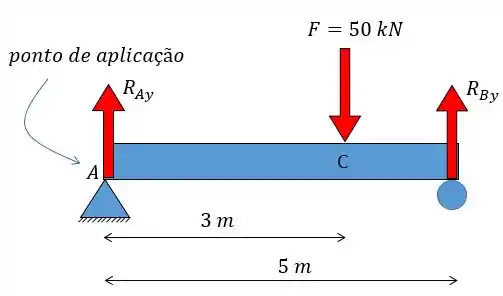
Perceba que as reações em desaparecem pelo fato de estarmos aplicado o momento no ponto . Por isso que para acharmos um valor a gente tem que sempre utilizar o ponto de aplicação onde já existe uma incógnita (na verdade, quanto mais incógnitas melhor). Continuando nós vamos ter:
Logo, substituindo na equação da força vertical:
Viu que maneiro! Achamos as nossas reações e podemos colocar elas na nossa viga:
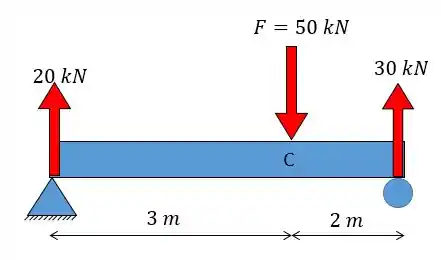
Forças distribuídas
Nos exemplos que vimos até aqui, as forças eram pontuais ou concentradas. Porém, muitas forças no mundo real são distribuídas. Essas forças podem ser substituídas por uma ou mais forças resultantes. Vamos ver os principais casos:
- Retangular ou uniforme:
- Triangular:
- Trapezoidal:
Para achar a força resultante é só calcular a área do retângulo. Mas como vamos saber aonde posicionar a força resultante? É sempre no meio do comprimento (na metade da base do retângulo):
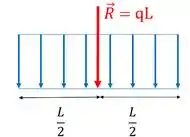
E olha só como vai ficar a força resultante nesse caso:
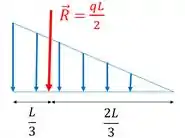
Não se esqueça que a resultante fica localizada a de distância da altura do triângulo. (Sempre no baricentro do triângulo)
Nesse caso, como vamos dividir o trapézio em um retângulo e em um triângulo para facilitar. A única diferença é que vamos ter duas forças resultantes.
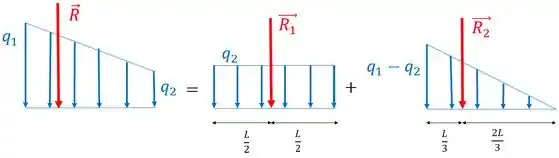
E o cálculo dessas forças resultantes, você faria olhando para o retângulo e para o triângulo, como foi mostrado lá em cima.
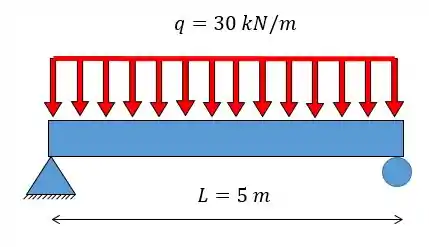
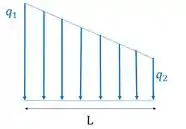
E se tivermos uma figura assim, onde representa a função da carga distribuída?
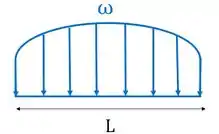
As forças distribuídas são dadas em unidades de força por comprimento (. Então, para achar a força resultante é só integrar a equação do carregamento ao longo do seu comprimento:
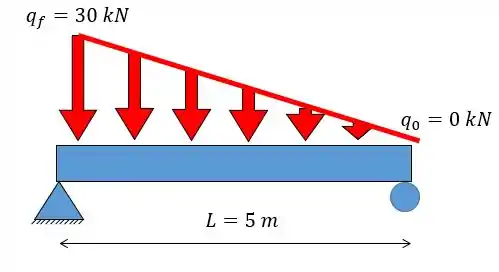
Se e está atuando numa viga de , por exemplo, vamos ter que:
Nos casos anteriores, a resultante está localizada no centroide da figura. Mas e nesses casos mais gerais como faço para saber a localização da resultante? Para isso vamos usar essa fórmula aqui:
Aonde, resolvendo a integral teríamos:
E substituindo os limites de integração
E com isso, nosso ponto de aplicação da força seria:
Pessoal, vamos ver na prática como essas cargas uniformes funcionam então vamos para os exercícios!!