Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 101
101- Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuantes no elemento .
Passo 1
Vamos isolar o elemento do sistema e desenhar as forças nos pinos:
Mas antes vamos descobrir suas medidas.
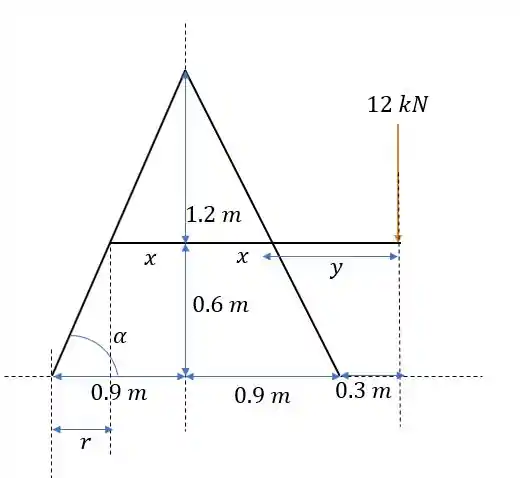
Pelo triângulo conseguimos tirar que:
E por semelhança de triângulos podemos tirar que:
Logo:
Logo:
Passo 2
Com essas distâncias podemos retirar as forças na barra .
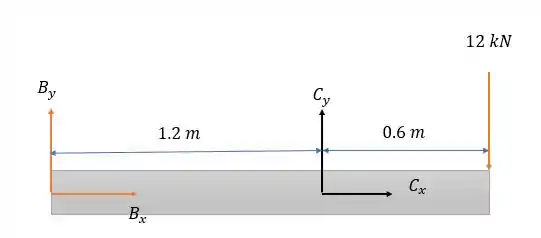
Fazendo a somatória dos momentos em temos:
Sentido para baixo na barra . E para cima na barra .
Pela somatória das forças verticais temos:
Pela somatória das forças horizontais temos:
Porém em temos um pino que faz reação normal a força na barra nos dando as seguintes reações.
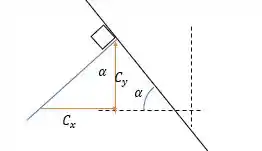
O pensamento é o mesmo que num plano inclinado, então dessa forma:
Dessa forma , sentido para a esquerda nessa barra mas na barra terá sentido para a direita.
Passo 3
Agora vamos analisar a estrutura toda:
Vamos encontrar as forças em fazendo o momento em :
Ou seja ela aponta para baixo. E como forças ativas não mudam de direção logo na barra ela terá esse sentido.
E pela somatória das forças verticais:
Pela somatória das forças horizontais temos que:
Passo 4
Agora vamos analisar as barras ligadas pelo ponto .
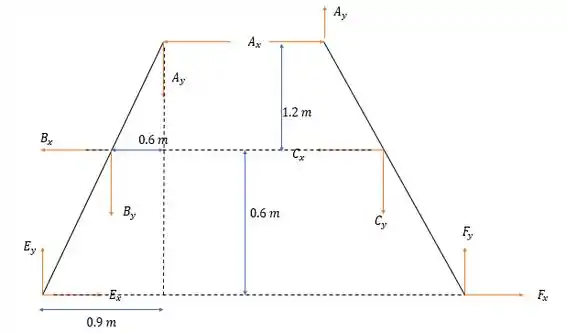
Fazendo a somatória dos momentos em na barra .
Substituindo o que já conhecemos:
Agora a somatória dos momentos em na barra .
Substituindo o que conhecemos:
Porém como e dos passos anteriores temos que:
O que faz sentido.
Fazendo a somatória das forças horizontais na barra temos:
E pela somatória das forças verticais é:
Apontando para baixo mesmo.
Juntando as duas equações em negrito com objetivo de eliminar nós teremos:
Ou:
Mas como do passo 1 encontramos
Então:
Sinal positivo, sentido para a esquerda (tal como desenhado).
E
Sentido para a esquerda
Resposta
Forças na barra