Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 113
113- Os elementos e são ligados por pinos em e sustentados por quatro hastes. Para o carregamento mostrado nas figuras, determine a força em cada haste.
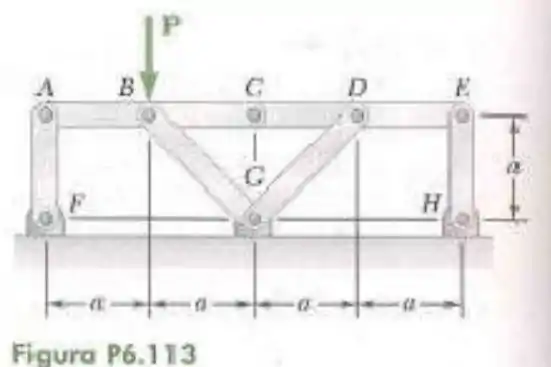
Passo 1
Uma forma de ver a estrutura da esquerda é:
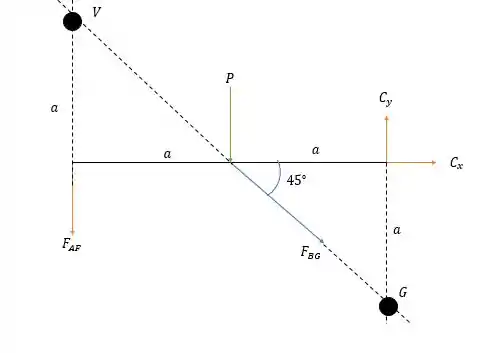
Assim não gera momento em ele também não gerará em .
Fazendo a somatória de momentos em temos:
Passo 2
Agora vamos para a estrutura da direita.
Fazendo a somatória dos momentos em teremos:
O que nos faz um sistema com:
O que dá:
Passo 3
Vamos voltar para essa estrutura aqui:
Fazendo a somatória das forças horizontai nós temos:
Força compressiva.
Agora fazendo a somatória das forças verticais:
Força compressiva também.
Passo 4
Agora falta o outro lado da estrutura.
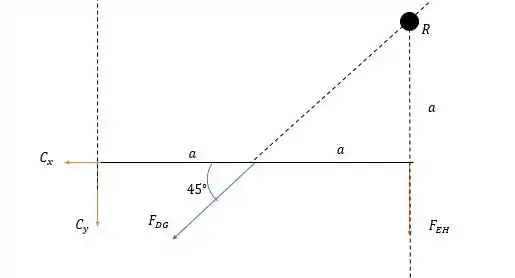
A soma das forças horizontais nos dá:
Força compressiva
E a soma das forças verticais:
Força de tração.
Resposta
Exercícios de Livros Relacionados
Determine os comprimentos de todas as forças atuantes no elemento A B C D quando θ = 0 °
Determine os componentes das reações em A e E quando uma força de 750N direcionada verticalmente para baixo é aplicada a em B , b em D .
Resolva o Problema 6.81 considerando que a carga de 18k N é substituída por um binário no sentido horário de intensidade 72k N ⋅ m aplicado ao elemento C D E F no ponto D .
Determine os componentes de todas as forças atuantes no elemento A B C D quando θ = 9 0 °
Para a estrutura e carregamento mostrados na figura, determine os componentes das forças exercidas no elemento A B C .