Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 103
103- Sabendo que e , determine os componentes das forças exercidas no elemento em e , no elemento em .
Passo 1
Analisando as forças nos contatos e pelo diagrama todo nós teremos:
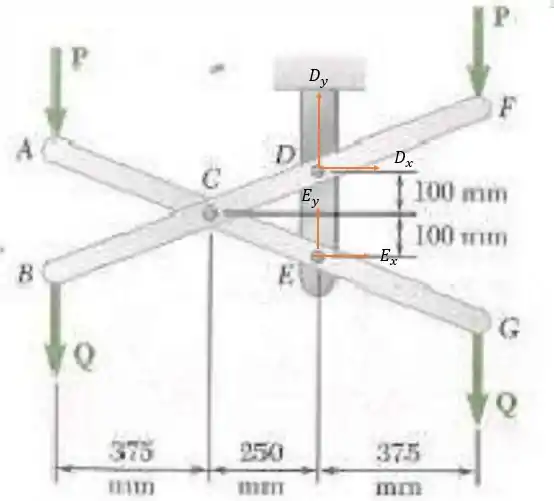
Pensa que estamos retirando a barra que une e e estamos apenas escancarando as forças ativas de e .
Fazendo a somatória de momentos em temos:
Sentido para a esquerda.
Dessa forma pela somatória das forças horizontais temos que:
Sentido para a direita.
Substituindo os valores de e teremos:
Passo 2
Agora vamos isolar a barra sabendo que as forças em não irão inverter.
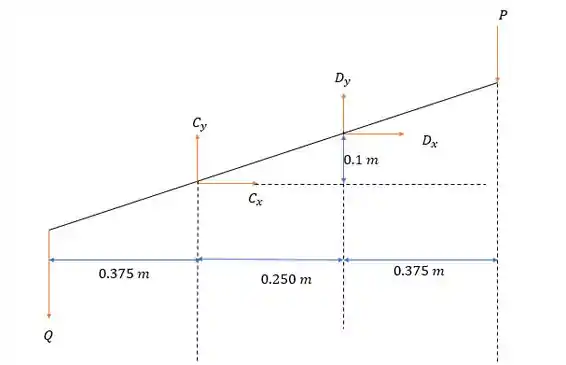
Pela somatória das forças horizontais temos que vale:
Sentido para a esquerda.
Agora fazendo a somatória dos momentos em .
Sentido para cima
Pela somatória das forças verticais temos:
Sentido para cima mesmo.
Substituindo os valores de e .
Passo 3
Agora vamos desenhar a barra sabendo que os sentidos em invertem.
Pela somatória das forças horizontais temos:
Sentido para esquerda
E pela somatória das forças verticais:
Sentido para cima
Substituindo os valores: