Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 114
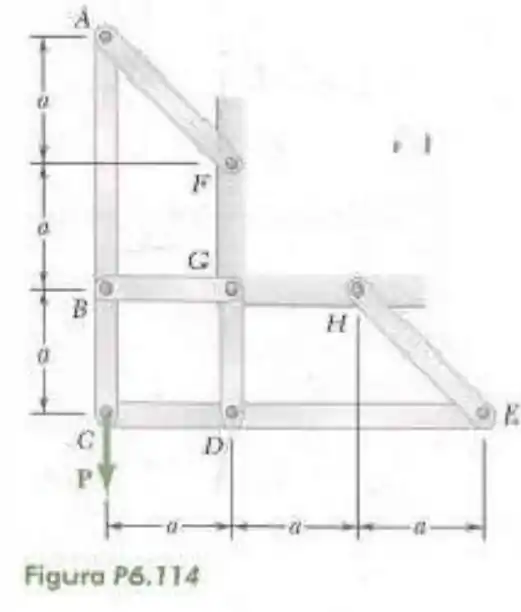
114- Os elementos e são ligados por pinos em e sustentados por quatro hastes e . Para o carregamento mostrado nas figuras, determine a força em cada haste.
Passo 1
O pino une as barras e e com isso a força é aplicado em somente uma dessas barras. Se formos colocar a força nas duas barras nós encontraremos valores dobrados e vamos considerar que essa força está na barra .
Fazendo a somatória dos momentos em temos:
Agora para a barra .
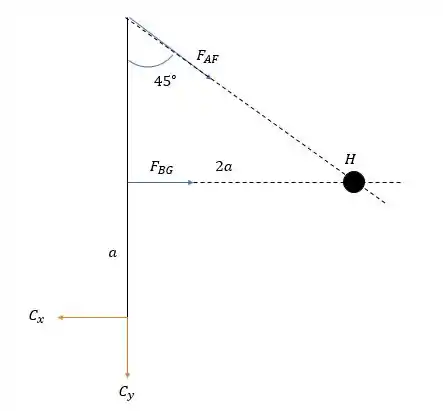
Com isso a somatória dos momentos em será:
Dessa forma utilizando a segunda equação na primeira nós teremos:
Logo:
Passo 2
Dessa forma podemos encontrar as forças nas hastes e que serão iguais a:
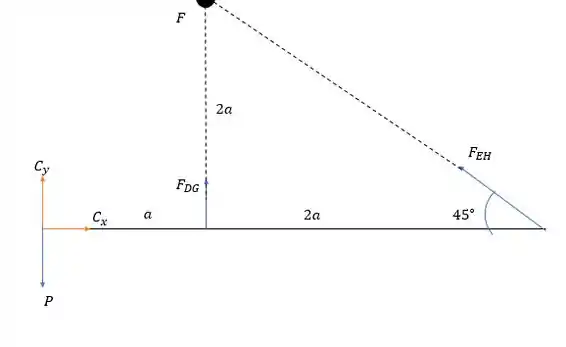
Pela somatória das forças verticais:
Força compressiva.
E fazendo a somatória das forças verticais:
Força trativa.
Passo 3
E para a outra barra:
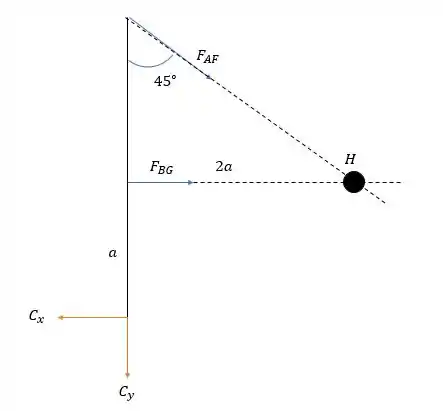
Pela soma das forças verticais:
Força trativa
E pela soma das forças horizontais:
Força compressiva