Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 109
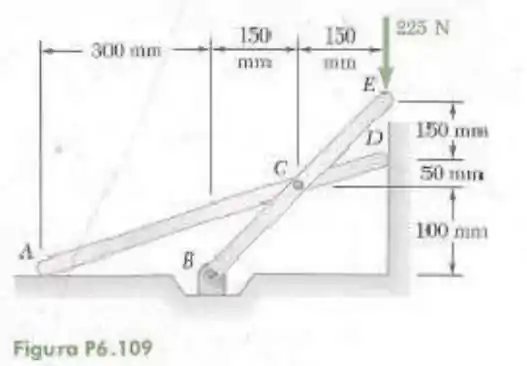
109- Sabendo que nas superfícies em e não há atrito, determine as forças exercidas em e no elemento .
Passo 1
Escrevendo as forças de equilíbrio no corpo todo (considerando que não há atrito horizontal em e nem vertical em ).
Fazendo a somatória dos momentos em nós teremos:
Passo 2
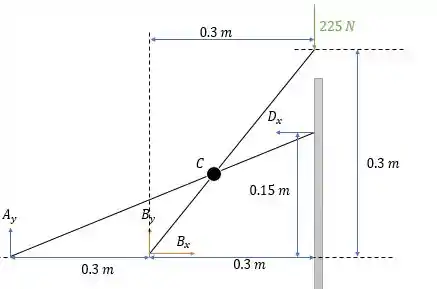
Agora analisando somente as forças na barra nós teremos:
Fazendo os momentos em nós temos:
O que nos dá :
E consequentemente:
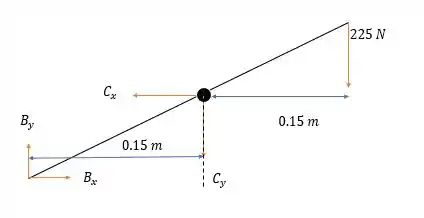
Dessa forma as reações em serão:
E
Então a força em terá módulo igual a:
Em um ângulo com a horizontal igual a:
Passo 3
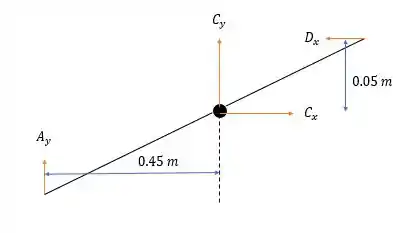
Agora para as forças na barra .
Com a somatória das forças horizontais, nós temos:
E pela somatória das forças verticais:
A força em terá um módulo igual a:
E um ângulo com a horizontal igual a:
Resposta
Exercícios de Livros Relacionados
A treliça mostrada na figura consiste em seis elementos e é sustentada por uma pequena haste de conexão em A, duas pequenas hastes de conexão em B e por uma rótula em D. Determine a força em cada um d
99- Para a estrutura e carregamento mostrados na figura, determine a força exercida no elemento C F E em C e F .
104- Sabendo que P = 110N e Q = 250N , determine os componentes das forças exercidas a ) no elemento B C D F em C e D , b ) no elemento A C E G em E .
100- Para a estrutura e o carregamento mostrados na figura, determine a força exercida no elemento D C E em C e D .
102- Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuantes no elemento A B E .