Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 112
112- Os elementos e são ligados por pinos em e sustentados por quatro hastes. Para o carregamento mostrado nas figuras, determine a força em cada haste.
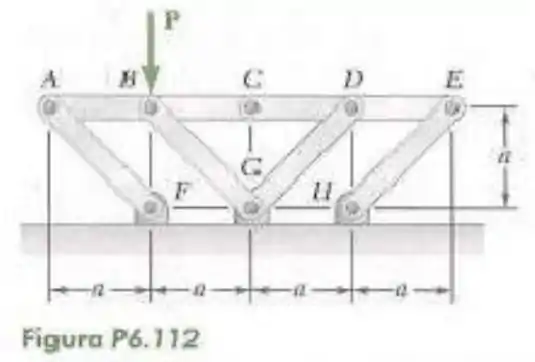
Passo 1
Desenhando o sistema de forças presente na estrutura a esquerda do pino em é:
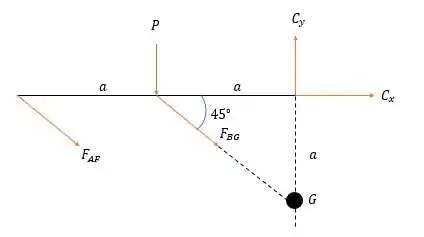
Se fizermos a somatória das forças verticais temos:
E agora fazendo a somatória das forças horizontais temos:
Somando as duas equações temos:
Passo 2
Agora vamos analisar as forças da estrutura a direita do pino .
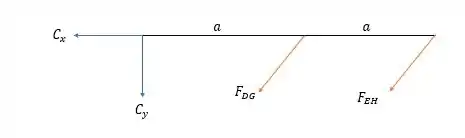
Fazendo a somatória das forças verticais nós temos:
E das horizontais:
Isso nos dá:
E se juntarmos com a equação encontrada no passo anterior nós temos:
Passo 3
Agora vamos observar essa estrutura de novo:
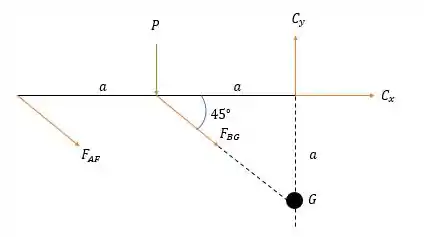
Se fizermos a somatória dos momentos em nós temos:
Substituindo o valor de nós teremos:
Força de tração
E se fizermos a somatória dos momentos em :
Passo 4
Agora para as forças da estrutura a direita.
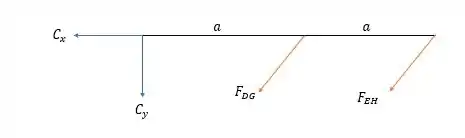
A somatória dos momentos em .
Força compressiva.
Pela somatória dos momentos em .
Força trativa.