Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 141

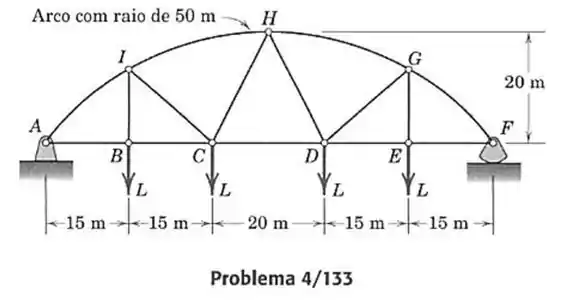
133- Determine as forças nos elementos A B , B I e C I da treliça simples. Observe que todos os elementos curvos são elementos de duas forças.

Passo 1

Analisando as forças externas, vamos calcular as reações nos apoios, considerando que as reações nos apoios temos que:

R a + R b = 4 L

E pela simetria da posição das forças podemos dizer que (se fizermos a somatória dos momentos em A acharemos a mesma resposta):

R a = R b = 2 L

Passo 2

Agora vamos separar uma metade da estrutura, traçar retas entre os pontos e colocar o centro desse arco na nossa figura. Precisamos encontrar os ângulos entre as barras para podermos encontrar as forças.

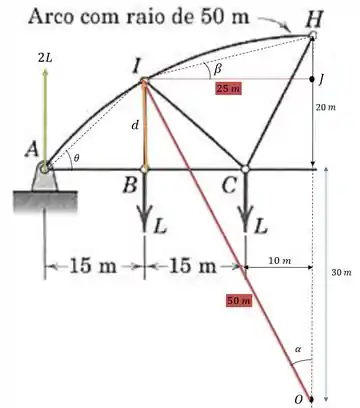
Da figura acima podemos calcular o valor de α ao fazer o seu seno, pois temos o seu valor de seno. Cujos tamanhos serão:

Cateto oposto: 25   m

Hipotenusa: 50   m

Logo α será:

α = sin - 1 ⁡   25 50 = 30 °

Agora podemos calcular o valor de O J . Essa medida vai ser importante para calcular os outros valores. Vamos calcular sua tangente.

t g   30 = 25 O J → O J = 43.30   m

Logo o valor de d será:

d = 43.30 - 30 = 13.30   m

Logo o valor de θ será:

t g   θ = d 15 → θ = 41.57 °

Agora podemos achar o valor de β .

H J = 20 - d = 6.7   m

Logo β será:

t g β = H J 25 → β = 15 °

Passo 3

Agora podemos encontrar o valor da força A B ao analisar o nó A .

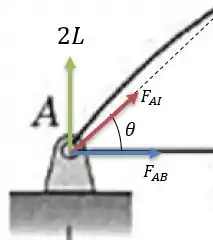
Fazendo a somatória das forças verticais ser nula nós encontramos:

2 L + F A I sin ⁡ θ = 0

F A I = - 2 L sin ⁡ θ

Substituindo o valor de θ a força será:

F A I = - 3.014 L

Agora fazendo a somatória das forças horizontais ser zero nós teremos:

F A I × cos ⁡ θ + F A B = 0

F A B = - F A I cos ⁡ θ

Agora substituindo os valores de F A I e de θ nós encontramos:

F A B = - - 3.014 L cos ⁡ 41.57 = 2.26 L

Como o valor é positivo logo essa força é de tração.

Passo 4

Se analisarmos a junta B vemos que:

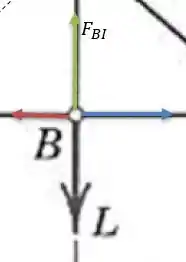
Nós vemos que se acharmos a somatória das forças verticais nós teremos:

F B I = L

Força trativa.

Passo 5

Agora analisando a junta I :

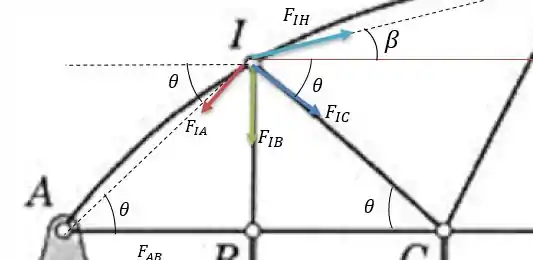
Já que o tamanho de A B e B C são iguais logo o triângulo A I C é isósceles então o ângulo I C ^ B é igual a θ e pela propriedade de ângulo temos que o ângulo formado entre a força F I C com a horizontal é de θ . Dessa forma podemos calcular a força na barra I C que falta.

Calculando a somatória das forças horizontais nós temos:

F I A cos ⁡ θ = F I H cos ⁡ β + F I C cos ⁡ θ

Substituindo os valores que conhecemos nós teremos:

- 3.014 L cos ⁡ 41.57 = F I H cos ⁡ 15 + F I C cos ⁡ 41.57

Agora fazendo a somatória das forças verticais:

F I H sin ⁡ β = F I A s i n   θ + F I C sin ⁡ θ + F I B

Substituindo os valores que conhecemos temos:

F I H sin ⁡ 15 = - 3.014 L s i n   41.57 + F I C sin ⁡ 41.57 + L

Resolvendo esse sistema nós encontramos:

F I C = 0.457 L   T

Resposta

F A B = 2.26 L   T

F B I = L   T

F I C = 0.457 L   T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

111- Os elementos A B C e C D E são ligados por pinos em C e sustentados por quatro hastes. Para o carregamento mostrado nas figuras, determine a força em cada haste.
Para a estrutura e carregamento mostrados na figura, determine a força exercida no elemento A B C a em B , b em C .
Classifique cada uma das estruturas mostradas nas figuras como complenamente, parcialmente ou impropriamente vinculada, se completatamente vinculada, classifique-a também como determinada ou indetermi
Classifique cada uma das estruturas mostradas nas figuras como complenamente, parcialmente ou impropriamente vinculada, se completatamente vinculada, classifique-a também como determinada ou indetermi
Resolver o Problema 6.77 quando theta = 150 ° .