Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 76
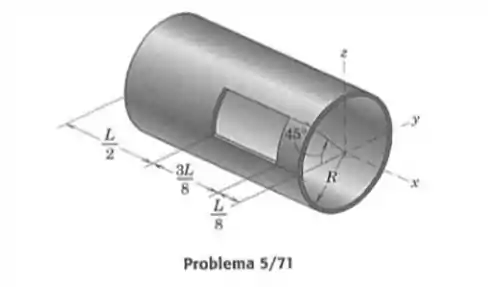
Determine a profundidade do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.
Passo 1
Questão bem bacana, que vai nos lembrar do que a gente vê lá no cálculo 1... mas calma gente, né nenhuma integral impossível de resolver não! Eis a seguir as formulinhas que devemos lembrar!
Vamos também entender como funciona o centro de massa dessa parte faltando! Vamos chamar o centro de massa desse buraco de .
Logo, para cada coordenada:
Passo 2
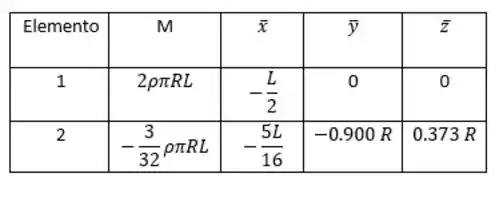
Agora, vamos dividir nosso problema em volumes, e a partir dai jogar na nossa formula! Mas antes, para organizar nosso pensamento, vamos montar uma tabela com valores!
Passo 3
Agora vamos montar a equação e matar a questão de vez!!
Resposta
Exercícios de Livros Relacionados
Determine a coordenada y do centróide da área sombreada. (Dica: consulte a solução do Problema 5/41.)
Determine as coordenadas do centro de massa do suporte, que é construído a partir de uma chapa de espessura uniforme.
O tanque de armazenamento de água é uma concha de revolução e deve ser pulverizado com duas camadas de tinta que tem uma cobertura de 500 pés2 por galão. O engenheiro (que se lembra da mecânica) consu
Determine a massa do comprimento de um quarto de círculo da mangueira do radiador. O diâmetro interno é 40 mm, a espessura da parede é 4 mm e a densidade do material de borracha é 1050 kg / m3.
A área de um quarto circular é girada 360 ° em torno do eixo y. Determine o volume do corpo resultante, que é uma parte de uma esfera.