Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 111
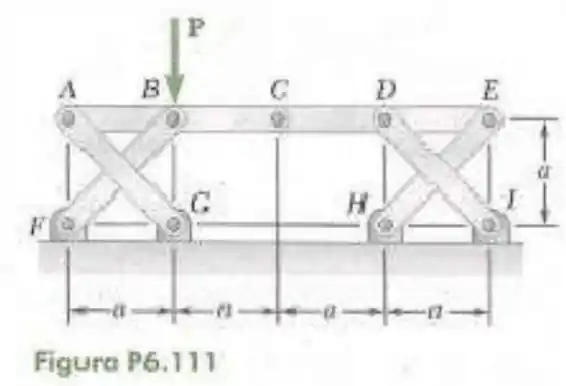
111- Os elementos e são ligados por pinos em e sustentados por quatro hastes. Para o carregamento mostrado nas figuras, determine a força em cada haste.
Passo 1
Para fazer essas questão vamos aplicar o método dos nós misturado com a separação do pino em da estrutura e com isso analisar o corpo a esquerda e a direita do mesmo.
Analisando o corpo a esquerda temos a força na haste e na haste .
Fazendo a somatória dos momentos em nós não precisamos nos preocupar com as forças nessas hastes agora:
Isso dá:
Passo 2
Agora analisando a estrutura a direita:
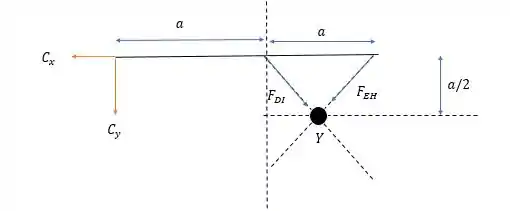
Fazendo a somatória dos momentos em nós temos:
Somando as duas equações temos:
Logo :
Passo 3
Agora que temos os valores de e de vamos voltar para a estrutura a esquerda.
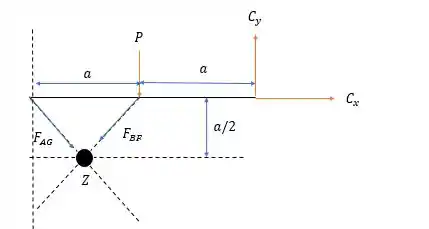
Agora vamos fazer os momentos no ponto é aplicado a força .
Pois os triângulos formandos tem catetos iguais a , formando ângulos de graus.
Como encontramos sinal negativo e colocamos a força entrando na barra , logo a força nessa haste é uma força compressiva.
Agora vamos fazer a somatória das forças verticais, que nos dará:
Força compressiva também
Passo 4
Agora vamos voltar de novo para a estrutura para a direita.
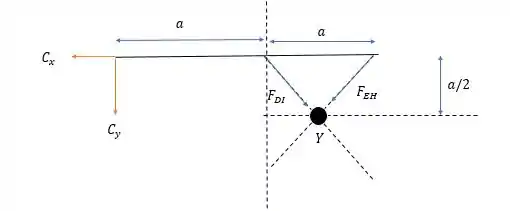
Pela somatória das forças verticais temos:
E pela soma das forças horizontais:
Isso nos dá um sistema igual a:
Somando as duas equações:
Força trativa.
Logo será:
Força compressiva.